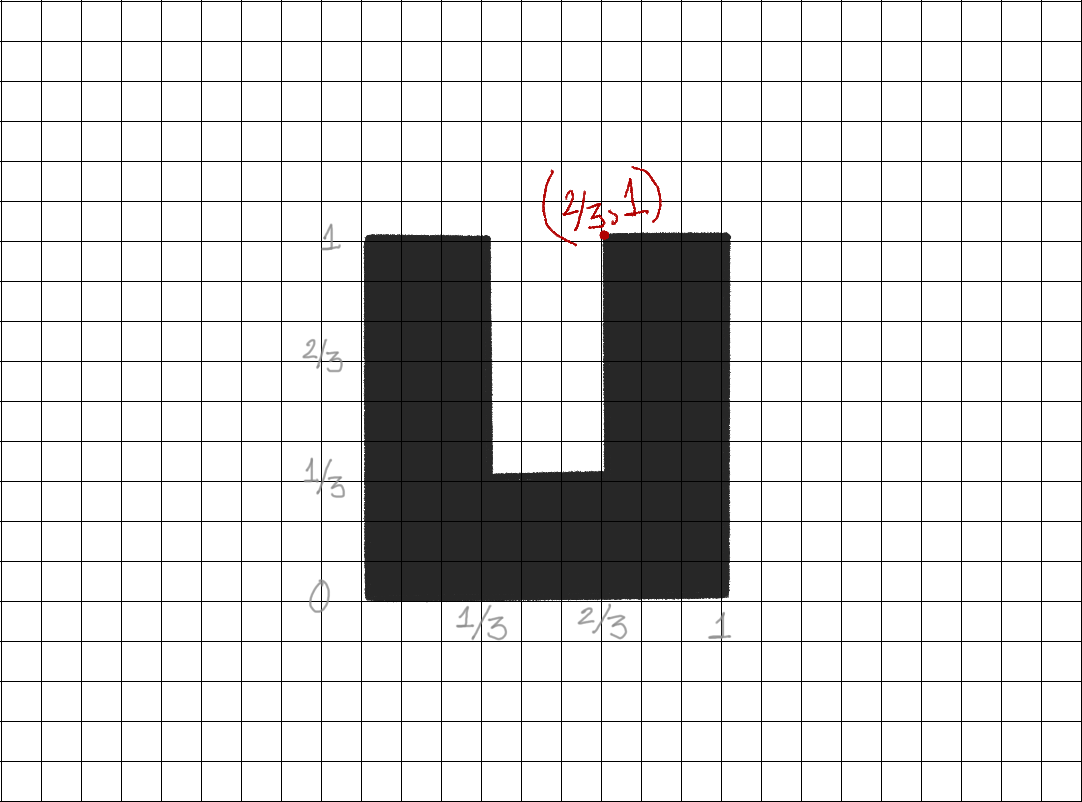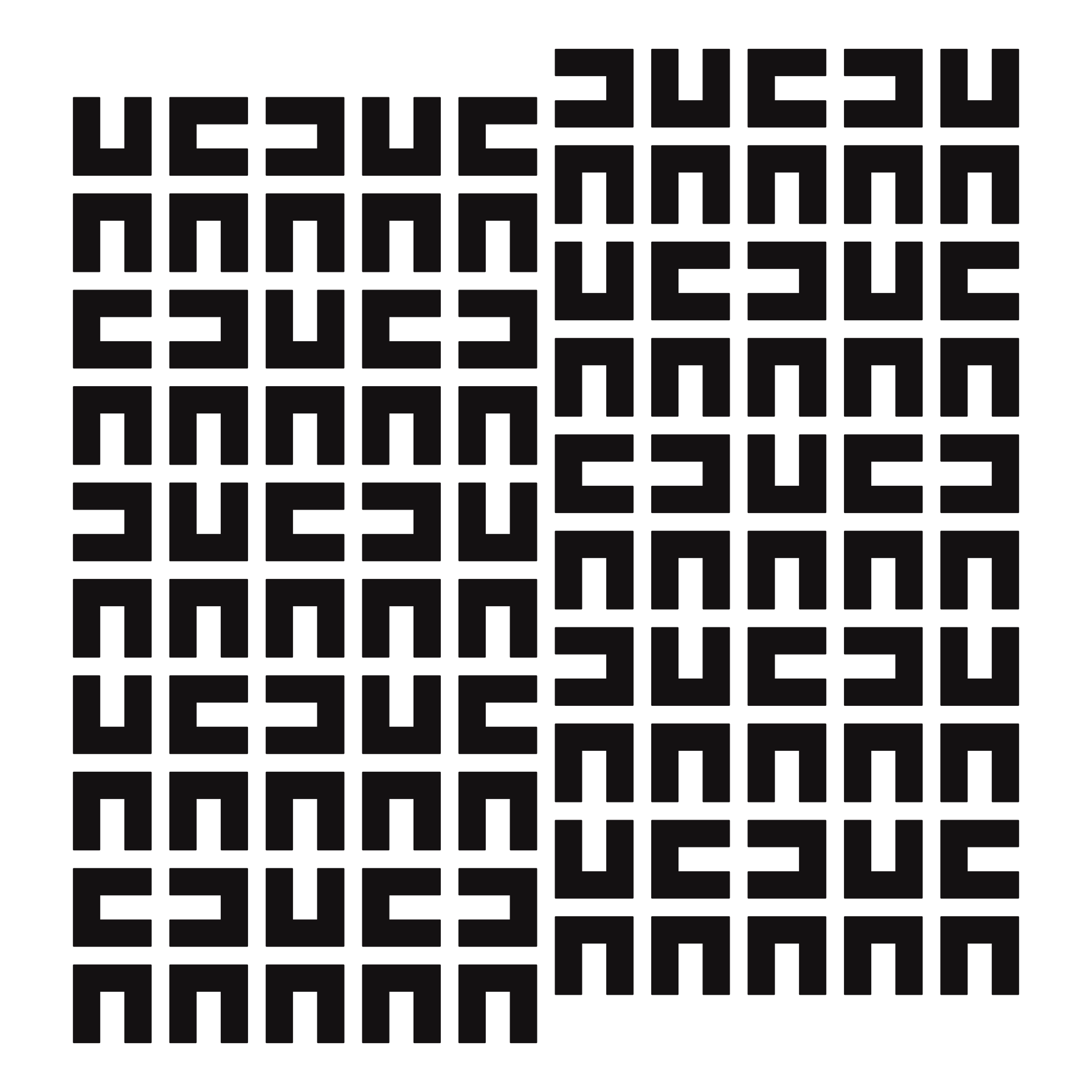Steal like an Rtist: Creative Coding in R
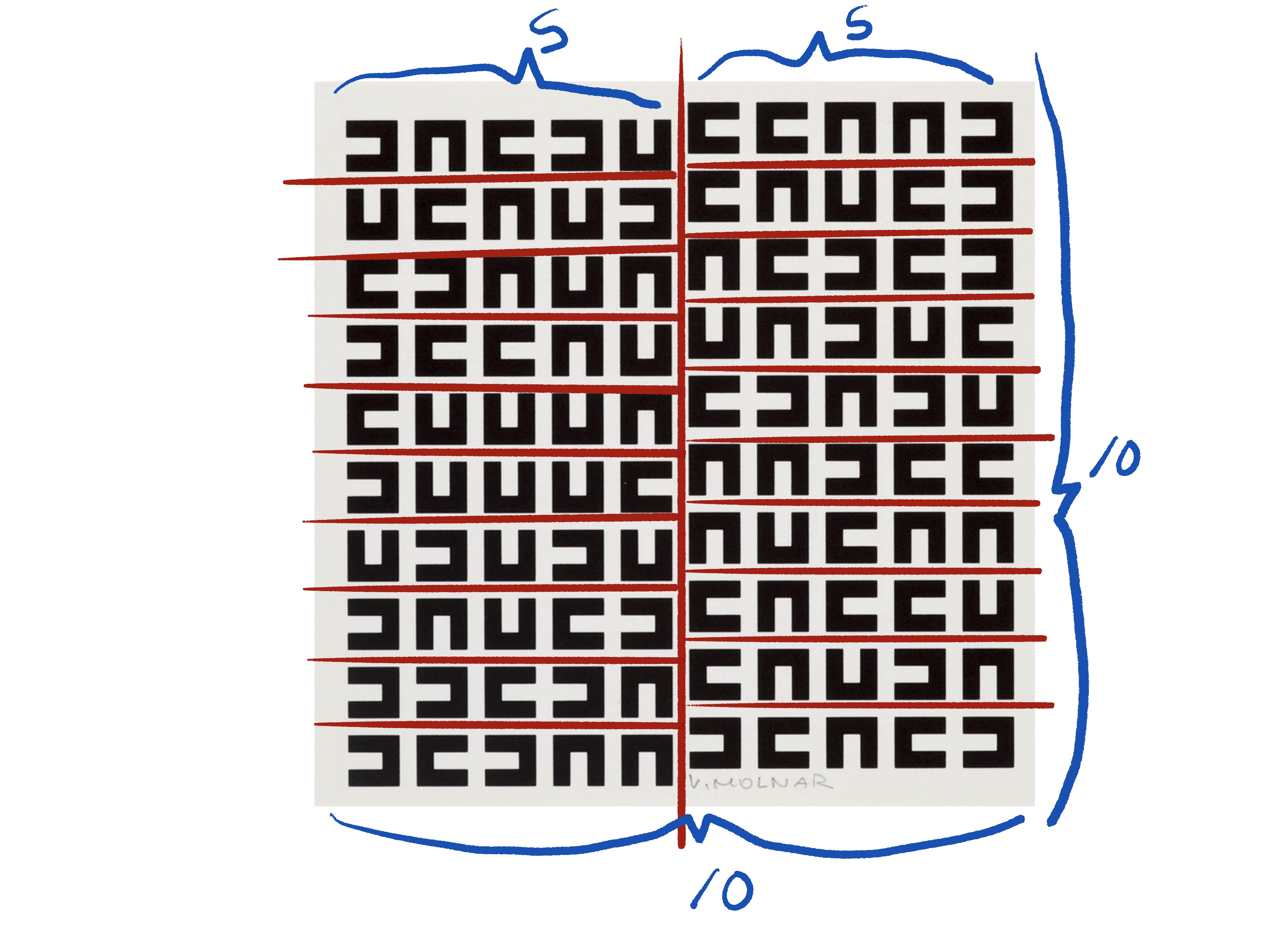
o.T. (carré noir)
Vera Molnár
Ijeamaka Anyene Fumagalli and Sharla Gelfand
posit::conf(2023)


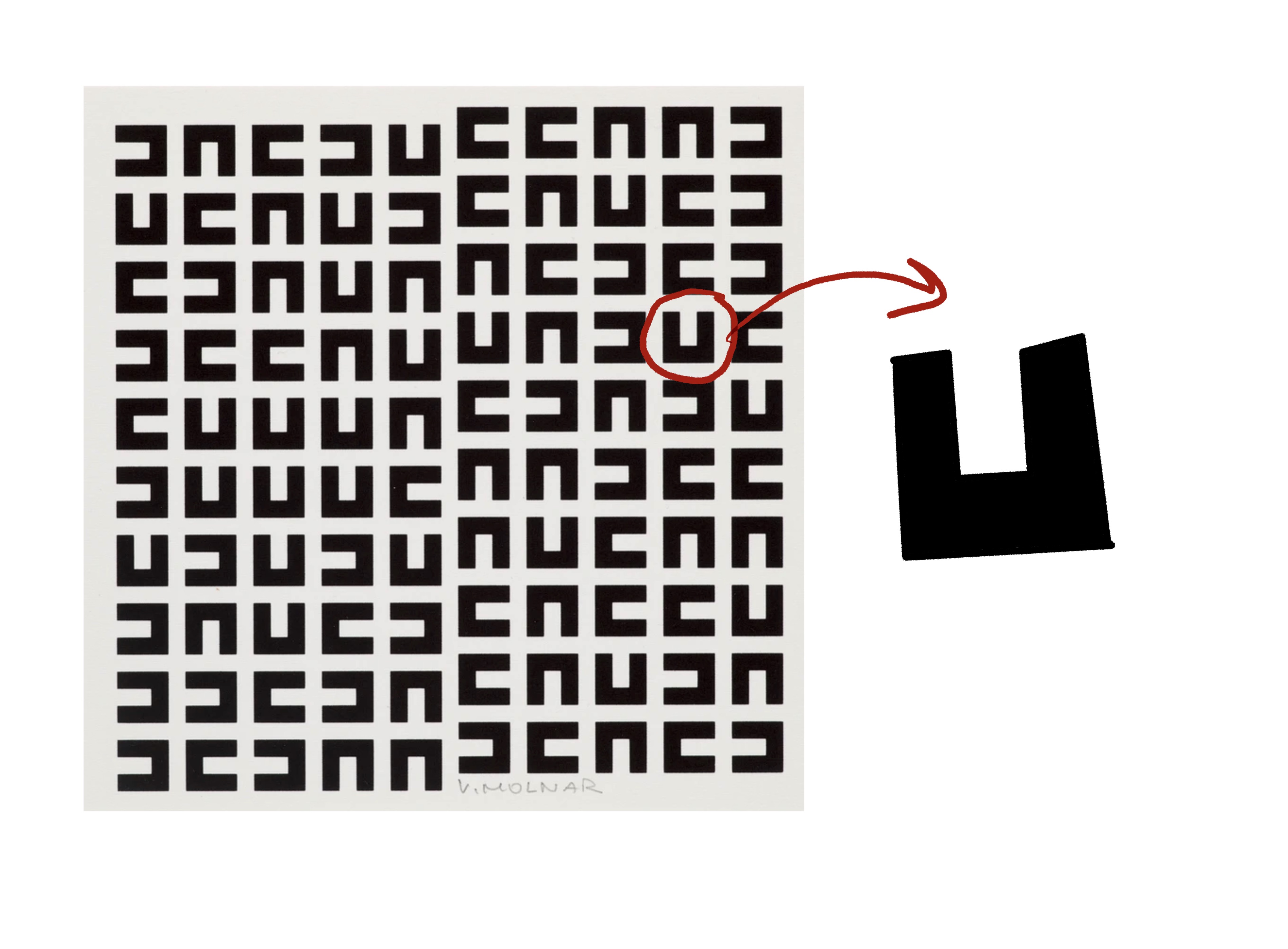
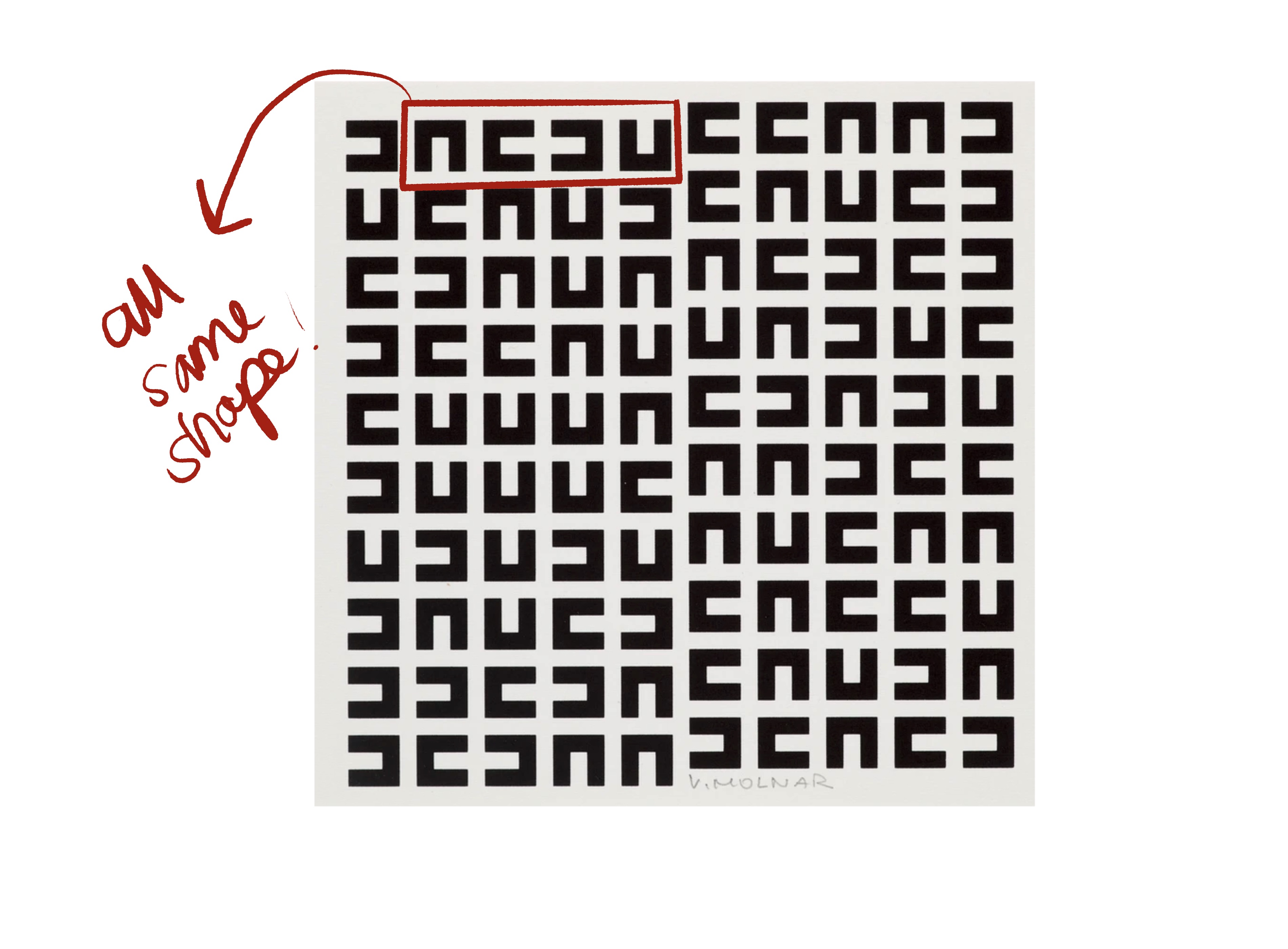
o.T. (carré noir): introduction to the shape
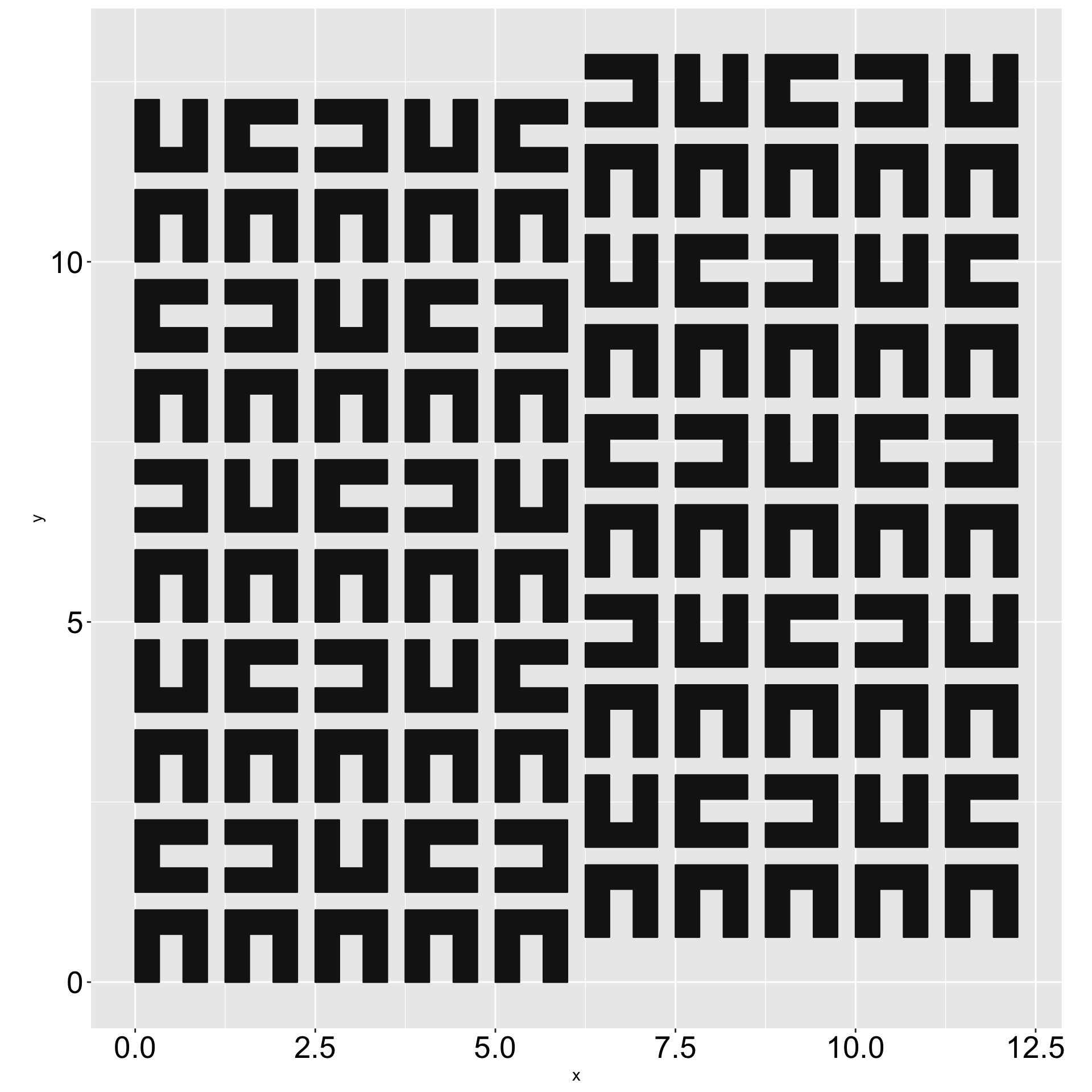
Orientation of the letter u
Composition of o.T. (carré noir)
Color palette

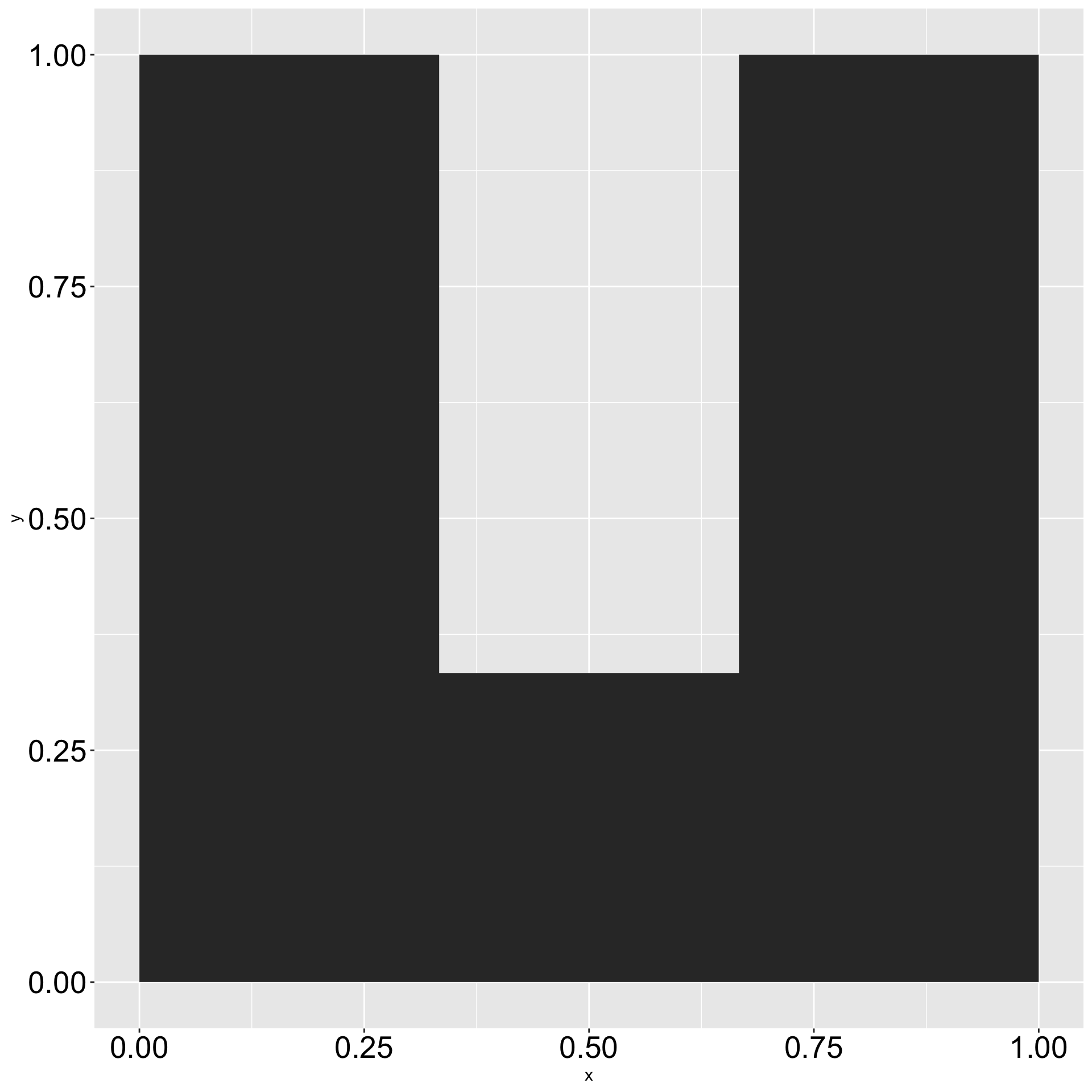
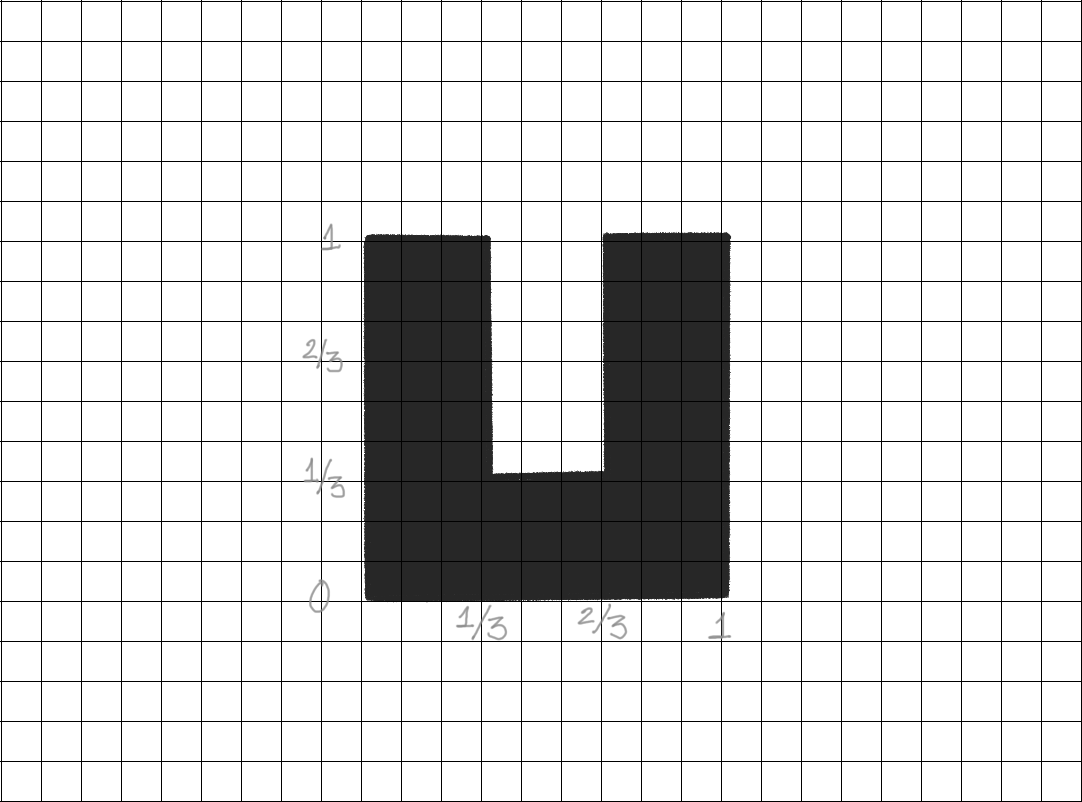
Creating Letter U
Creating polygons in {ggplot2}

Creating polygons in {ggplot2}
geom_polygon()
We will use the following aesthetics
- coordinates of data (
x,y) - color of the border of the polygon (
color) - color of the inside of the polygon (
fill) - which coordinates belong to which polygon (
group)
Creating polygons in {ggplot2}
geom_polygon()
We will use the following aesthetics
- coordinates of data (
x,y) - color of the border of the polygon (
color) - color of the inside of the polygon (
fill) - which coordinates belong to which polygon (
group)
geom_polygon() tips
Order of coordinates matters (a lot!)
Only coordinates of interest are the vertices
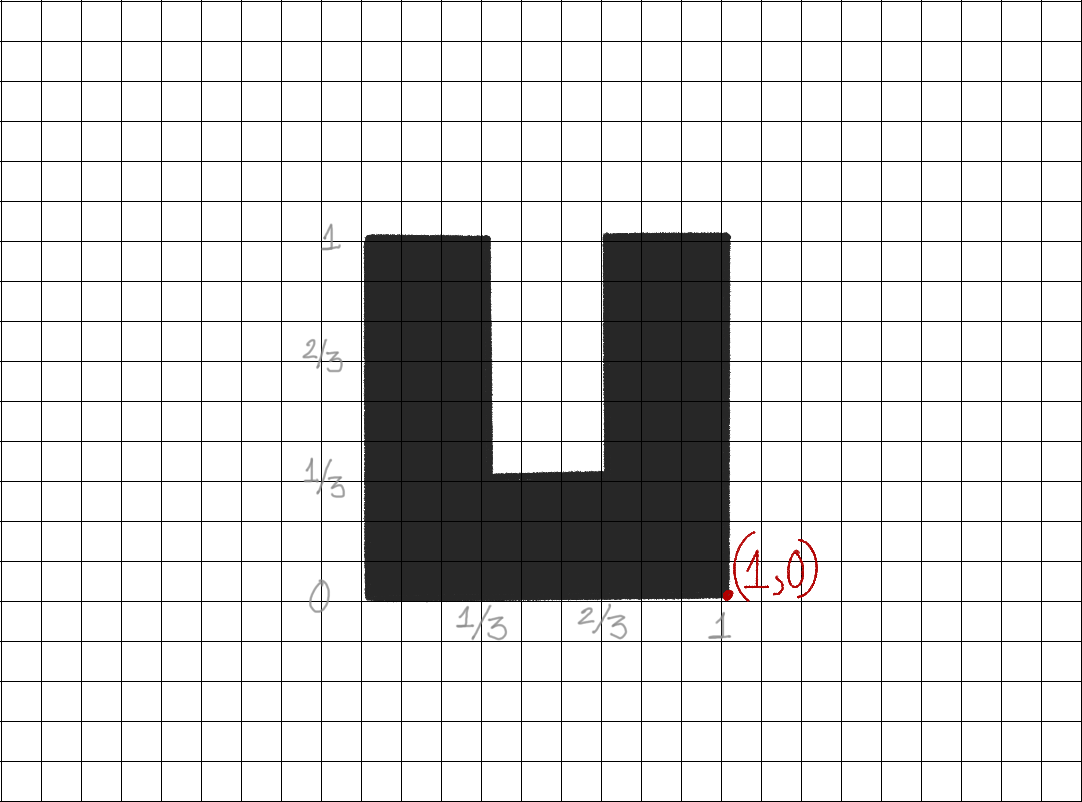
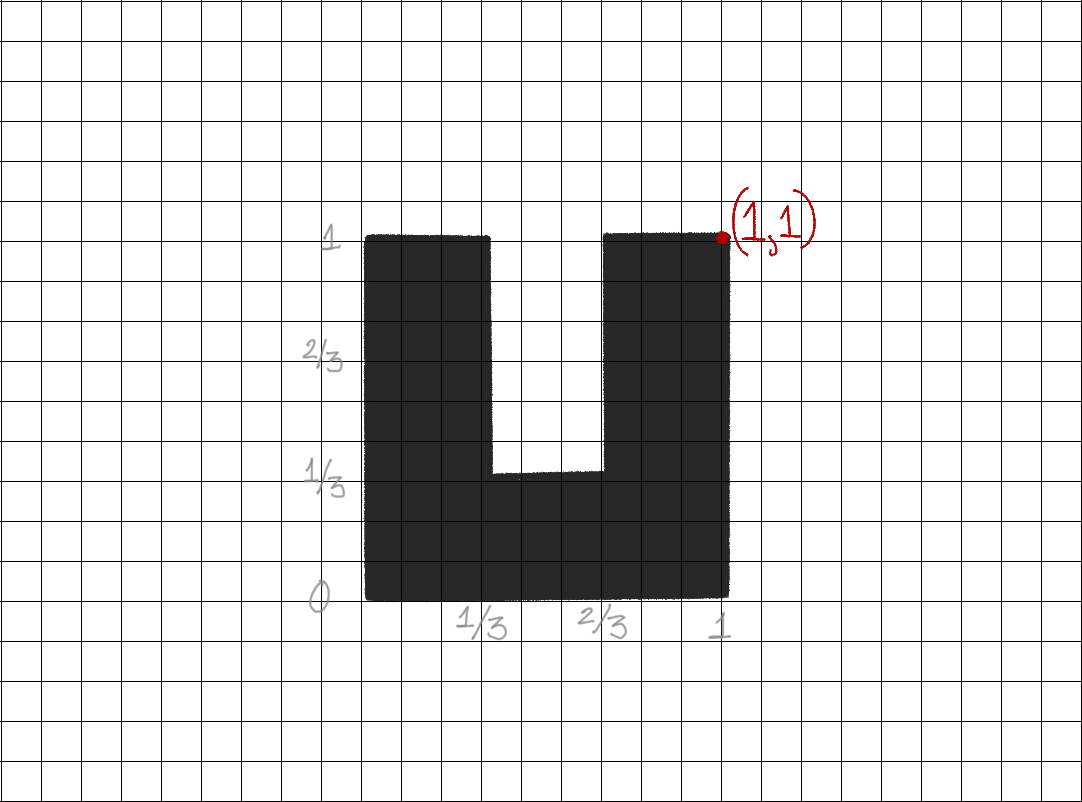
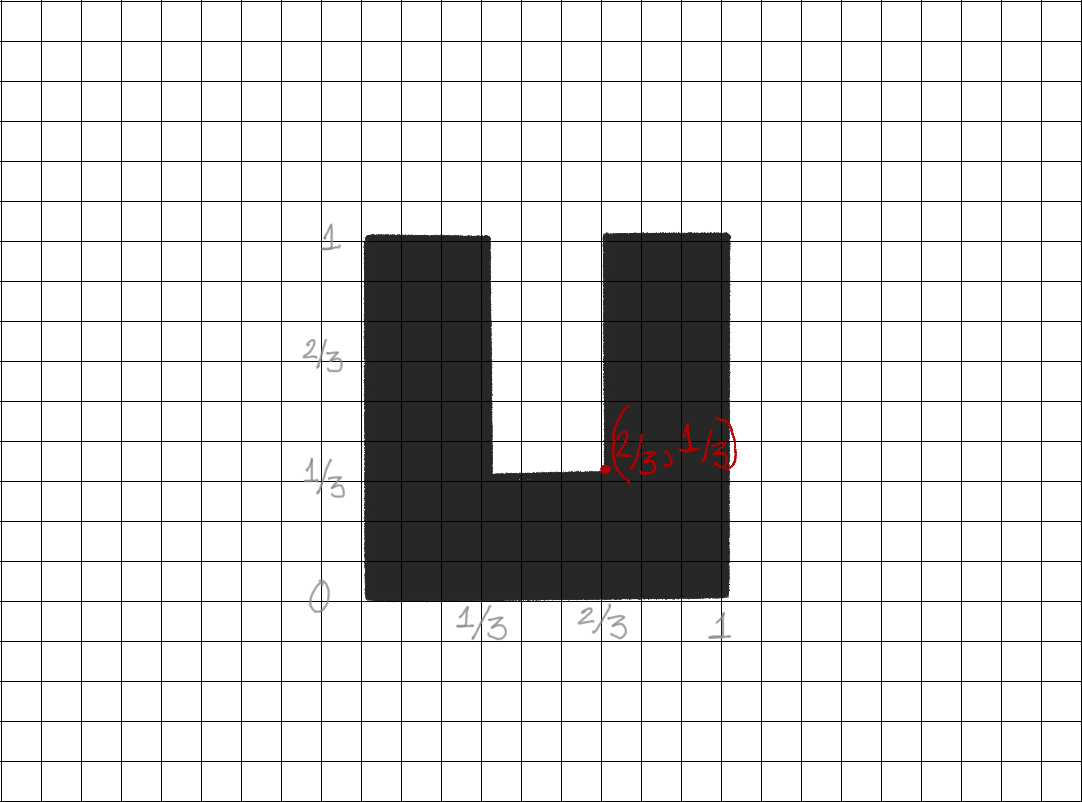
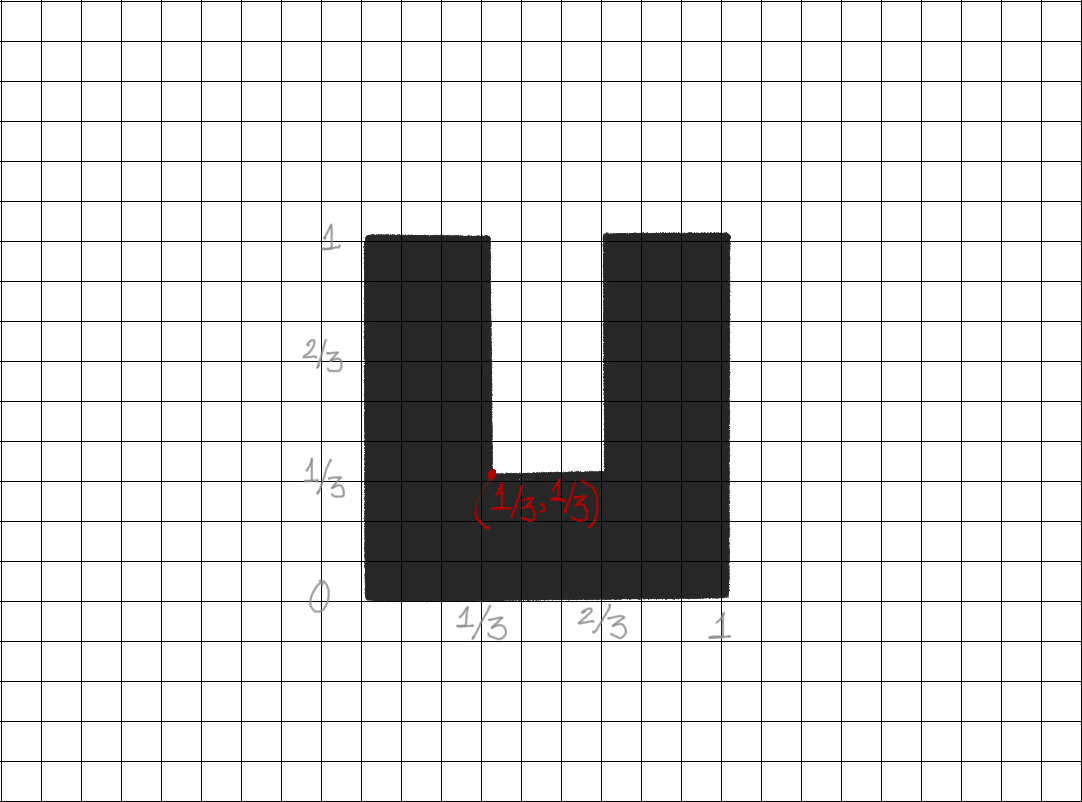
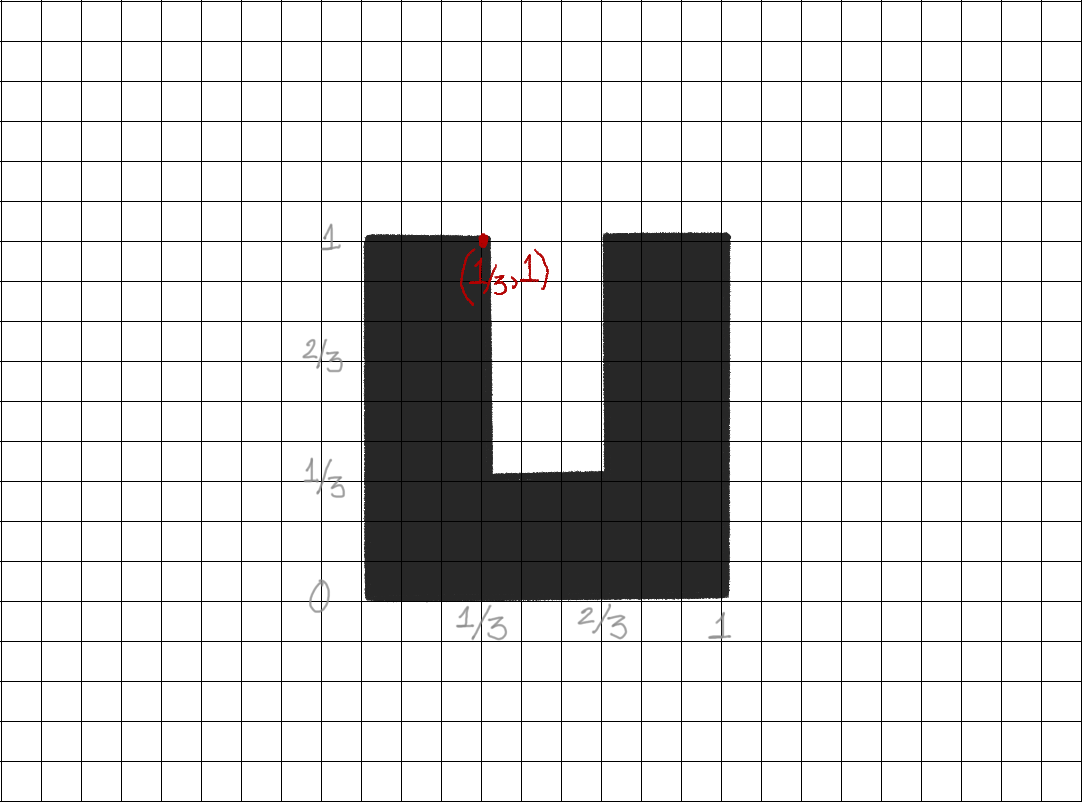
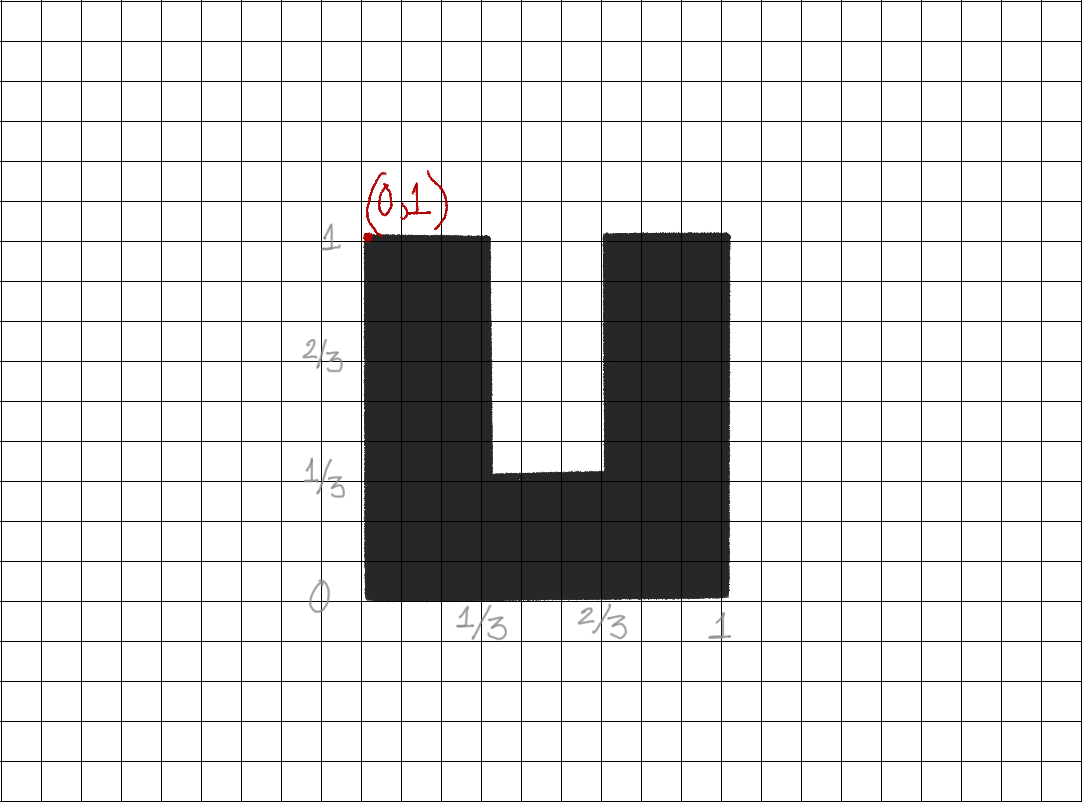
Coordinates of Letter U
Coordinates of Letter U
Go counterclockwise, starting from bottom left
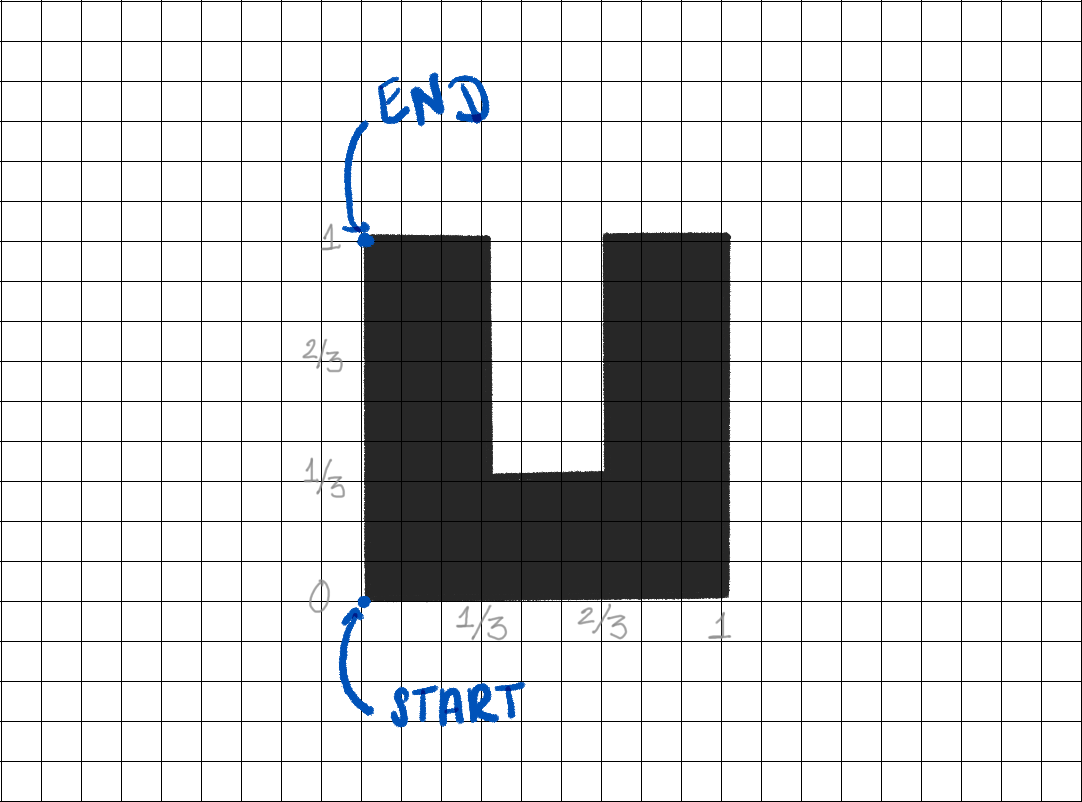
Coordinates of Letter U
Only need coordinates from vertices in the polygon
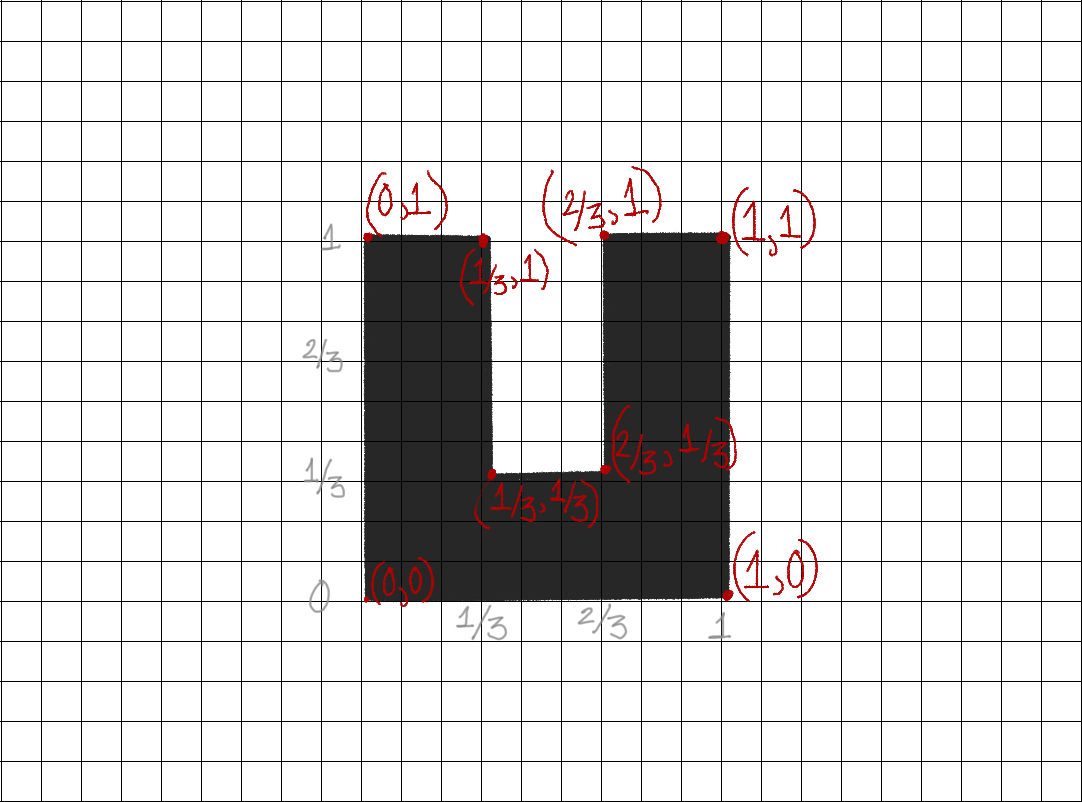
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Coordinates of Letter U
Plotting Letter U
Plotting Letter U
Plotting Letter U
Adding flexibility
Plotting Letter U
Adding flexibility
Plotting Letter U
Adding flexibility
Exercise 1
- Open file:
exercises/03-ot/exercise.Rmd - On your graphing paper, select from letters in
exercises/03-ot/letters/and draw out the letter. - Label all the vertices of the shape with the coordinates.
- Create a
tribble()with the coordinates of the letter you selected. - Create a new function,
create_letter(), that takesx0andy0as arguments and moves the shape according to those arguments. - Plot your shape at the
x0andy0of your choosing. - Share your output on Github discussion board.
- Remember to save your file when you are done with the exercise.
10:00
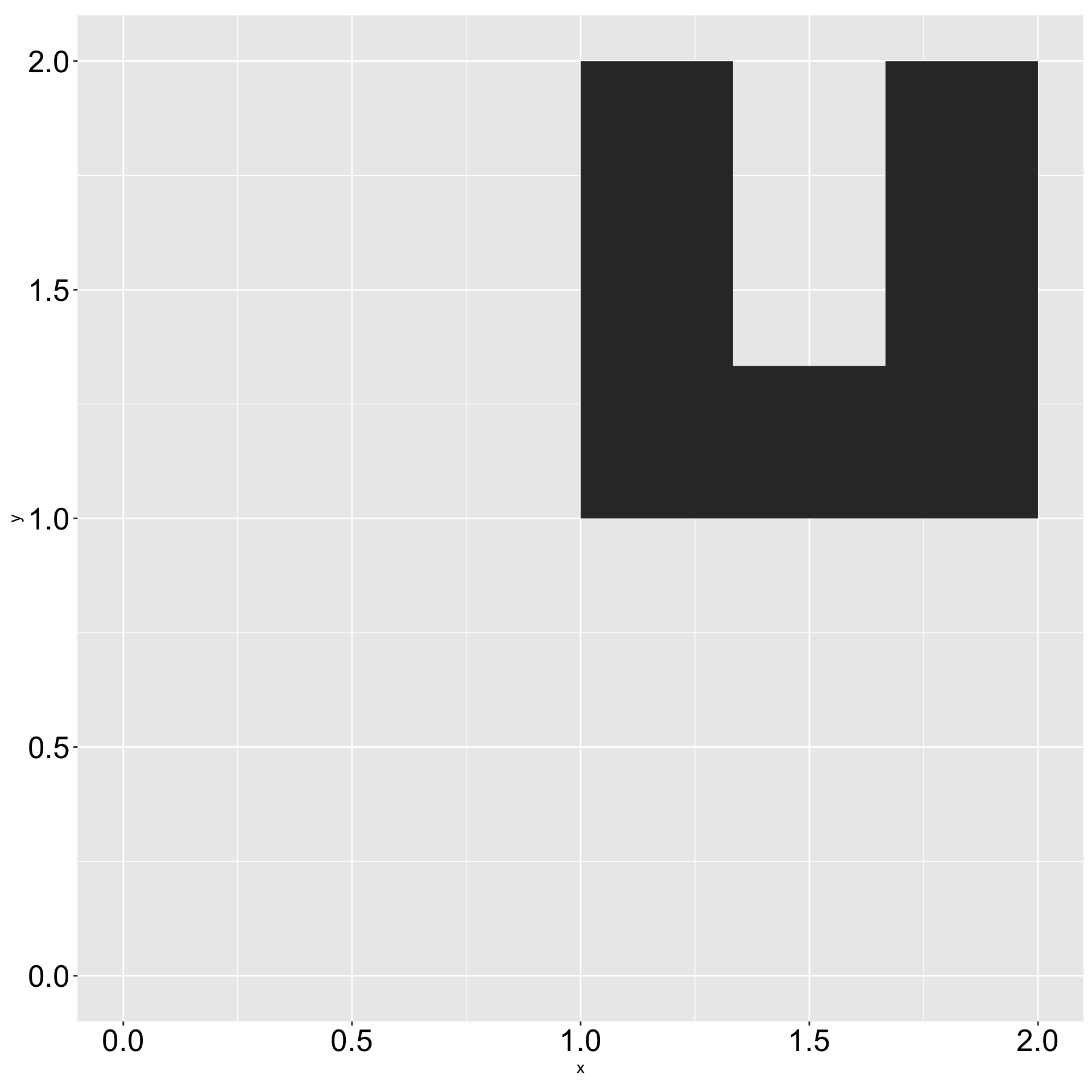
Orientation of the Letter U
Exploring Geometric Abstraction
“My life is in squares, triangles, lines”
Throughout her career, Vera Molnár experimented with repetitions and variations of letters, especially the letter M – as in Molnár.
She explored the balance between order and chaos.

A light trigonometry intermission
y_new = -x_old & x_new = y_old
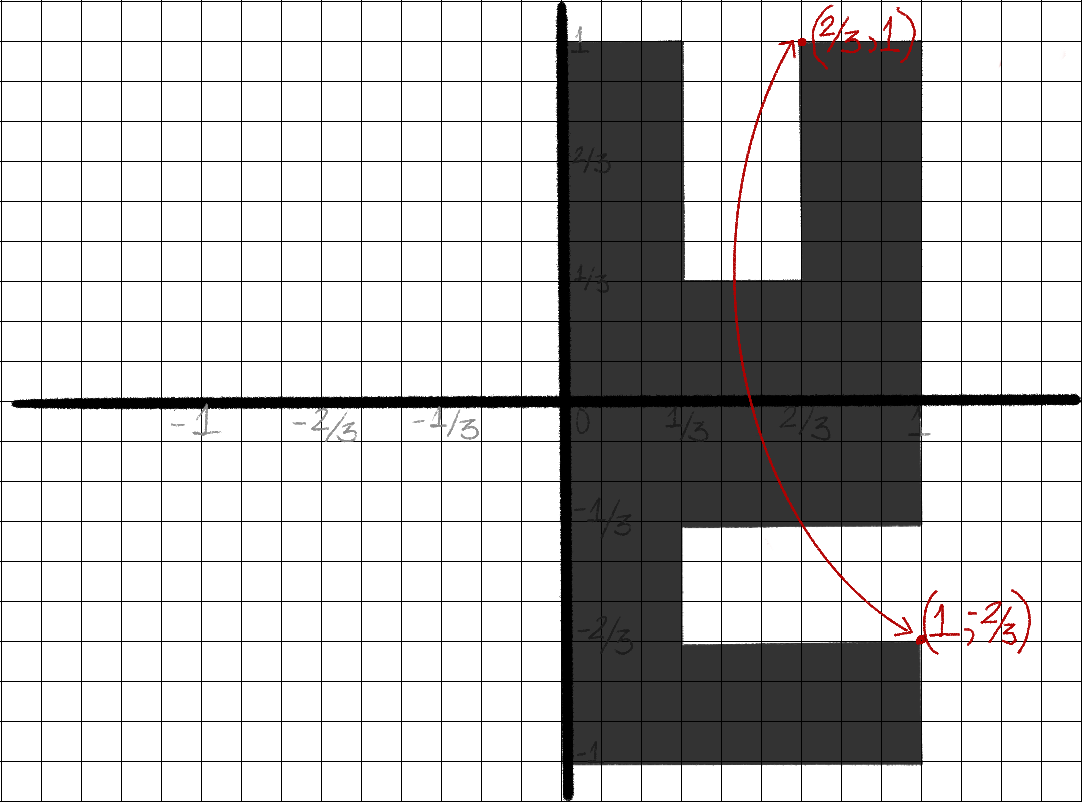
A light trigonometry intermission
y_new = -y_old & x_new = -x_old
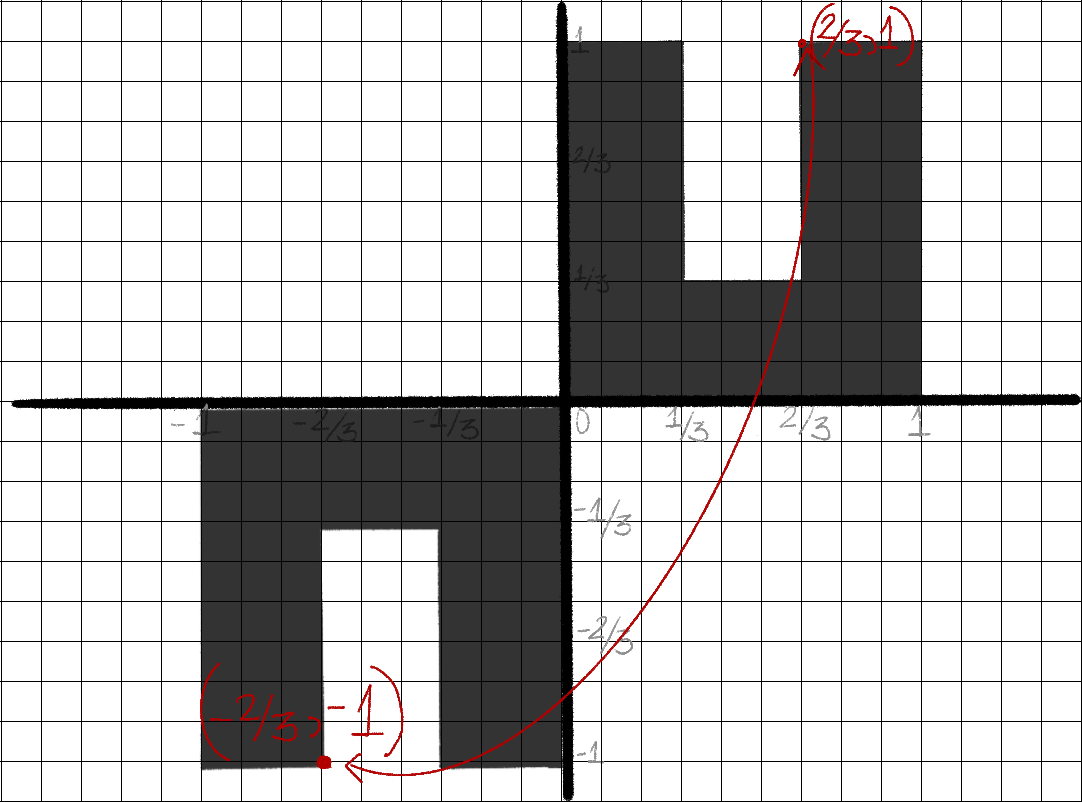
A light trigonometry intermission
y_new = x_old & x_new = -y_old
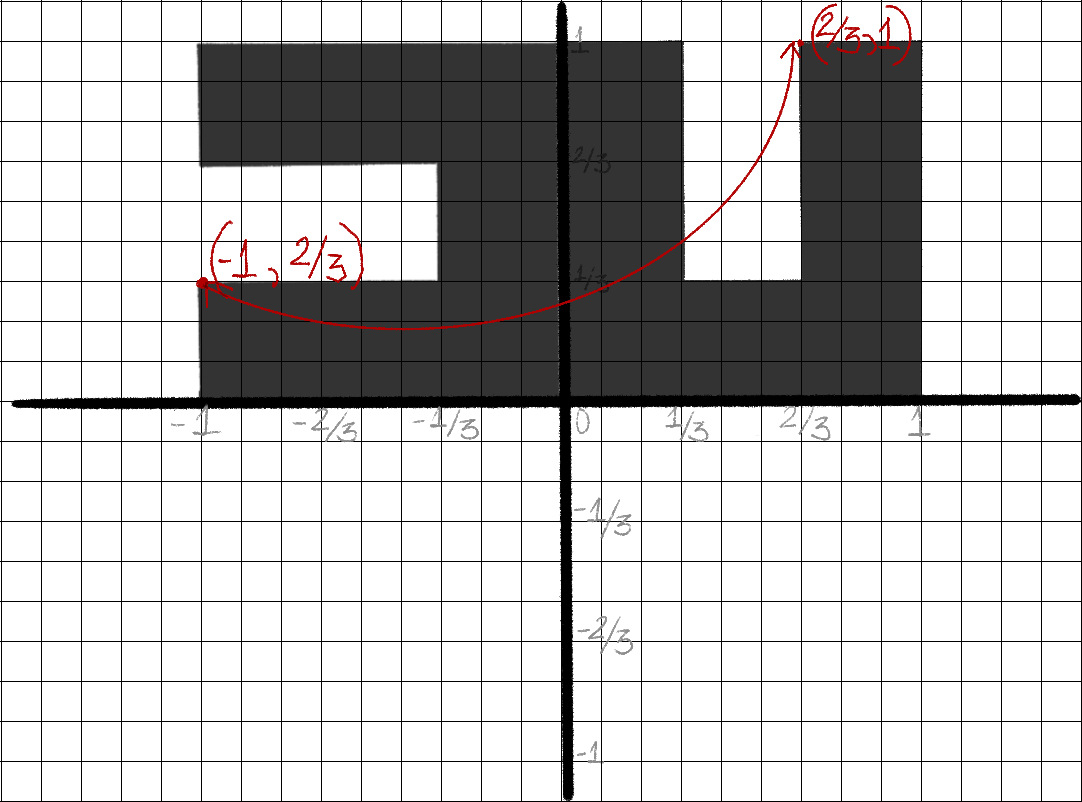
A light trigonometry intermission
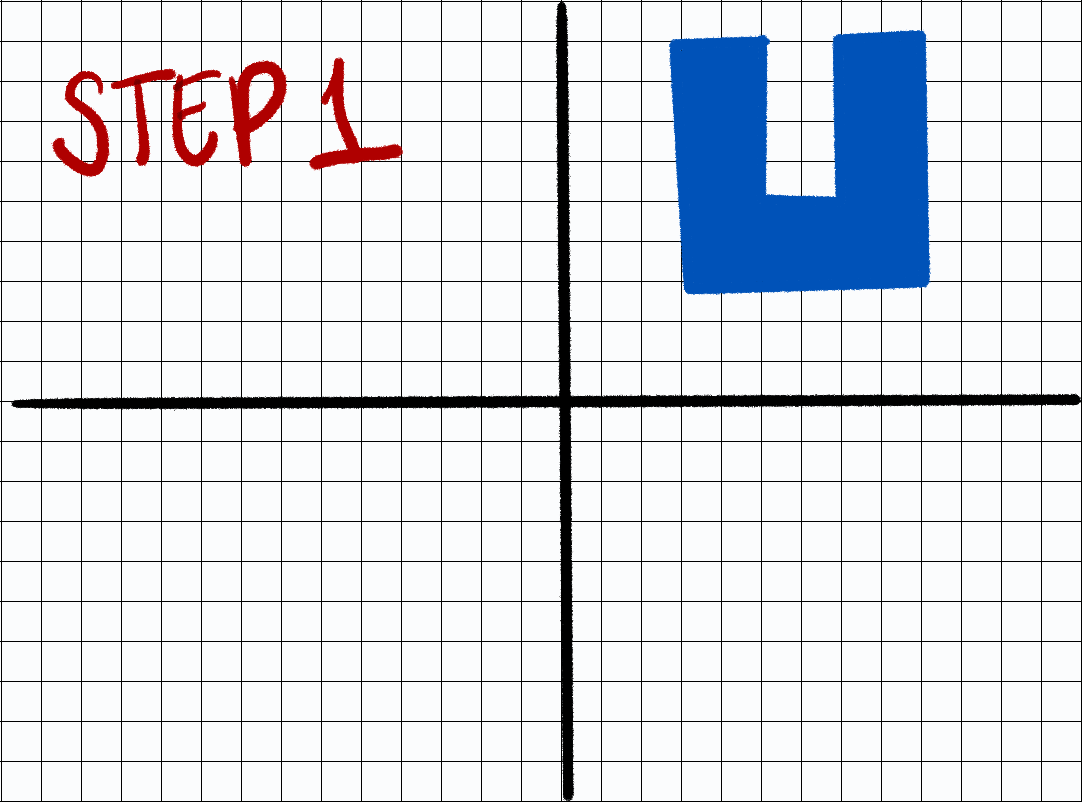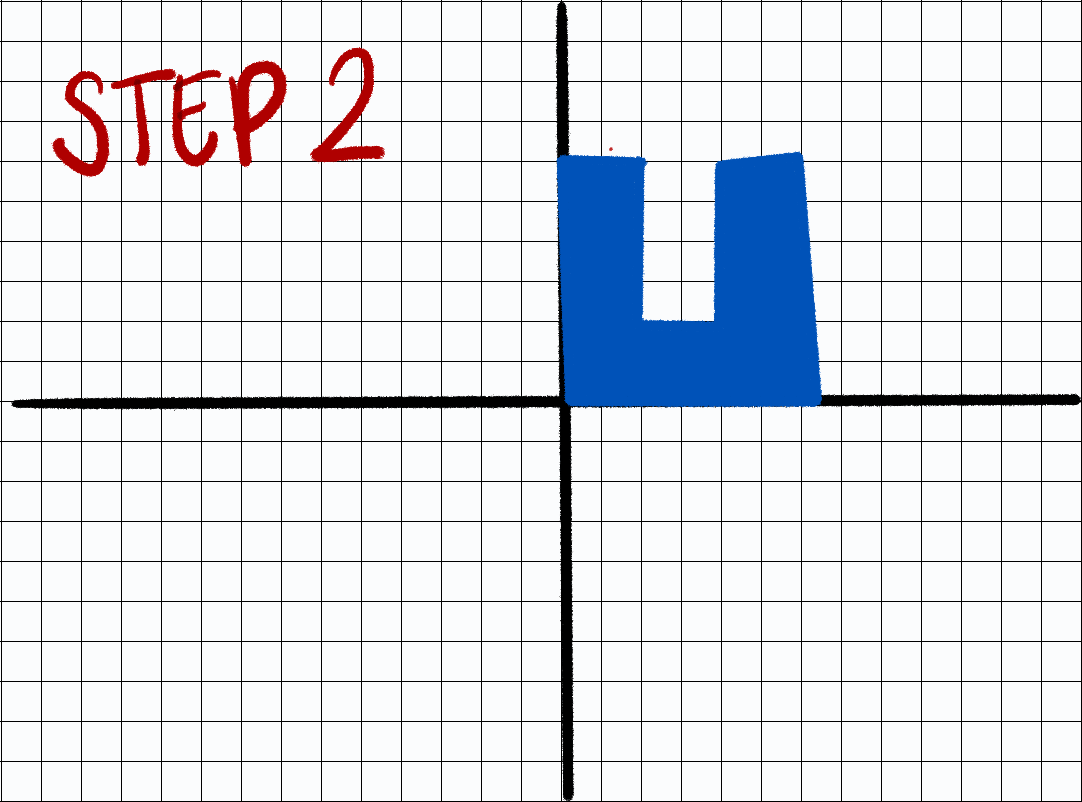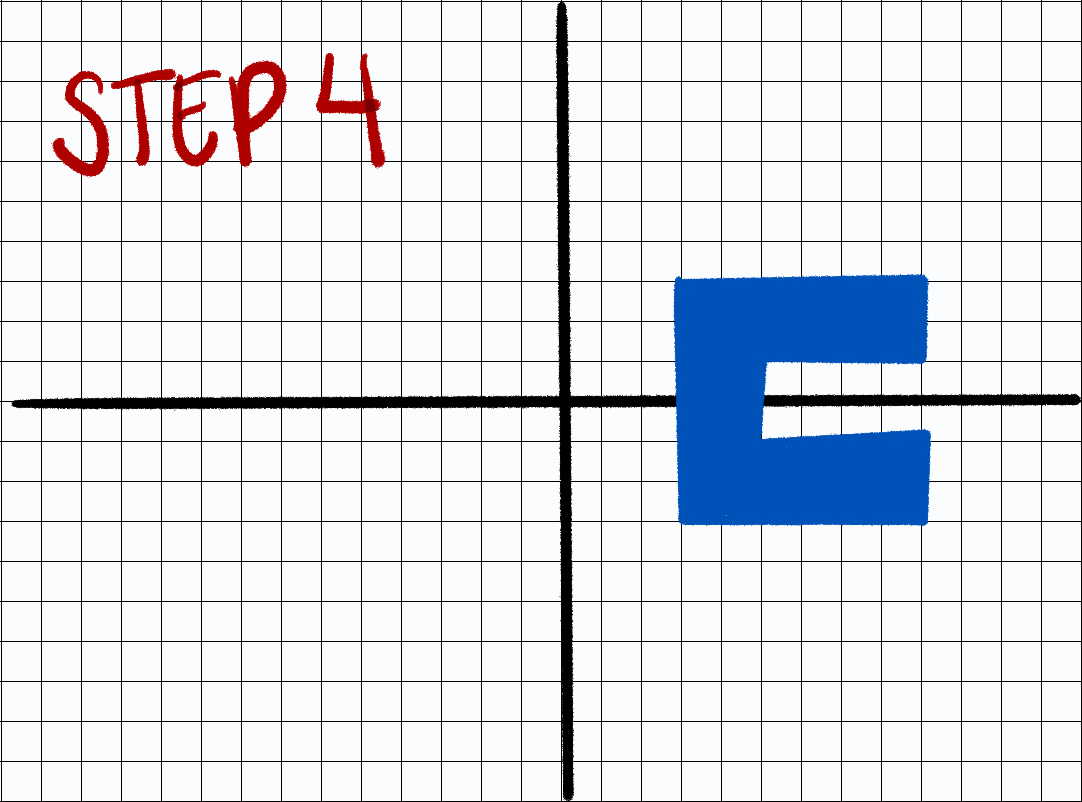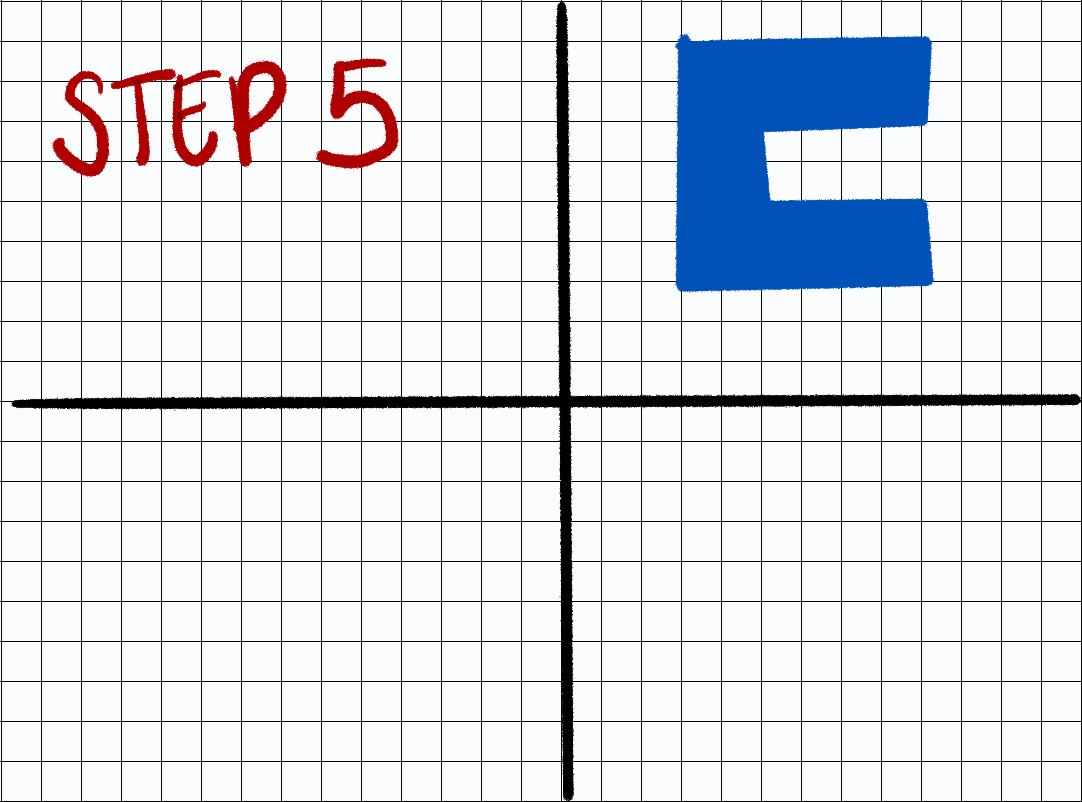
- Step 1: Place shape
- Step 2: Subtract point of rotation off of each vertex
- Step 3: Rotate
- Step 4: Add back point of rotation
- Step 5: Correct coordinates to back at “original origin”
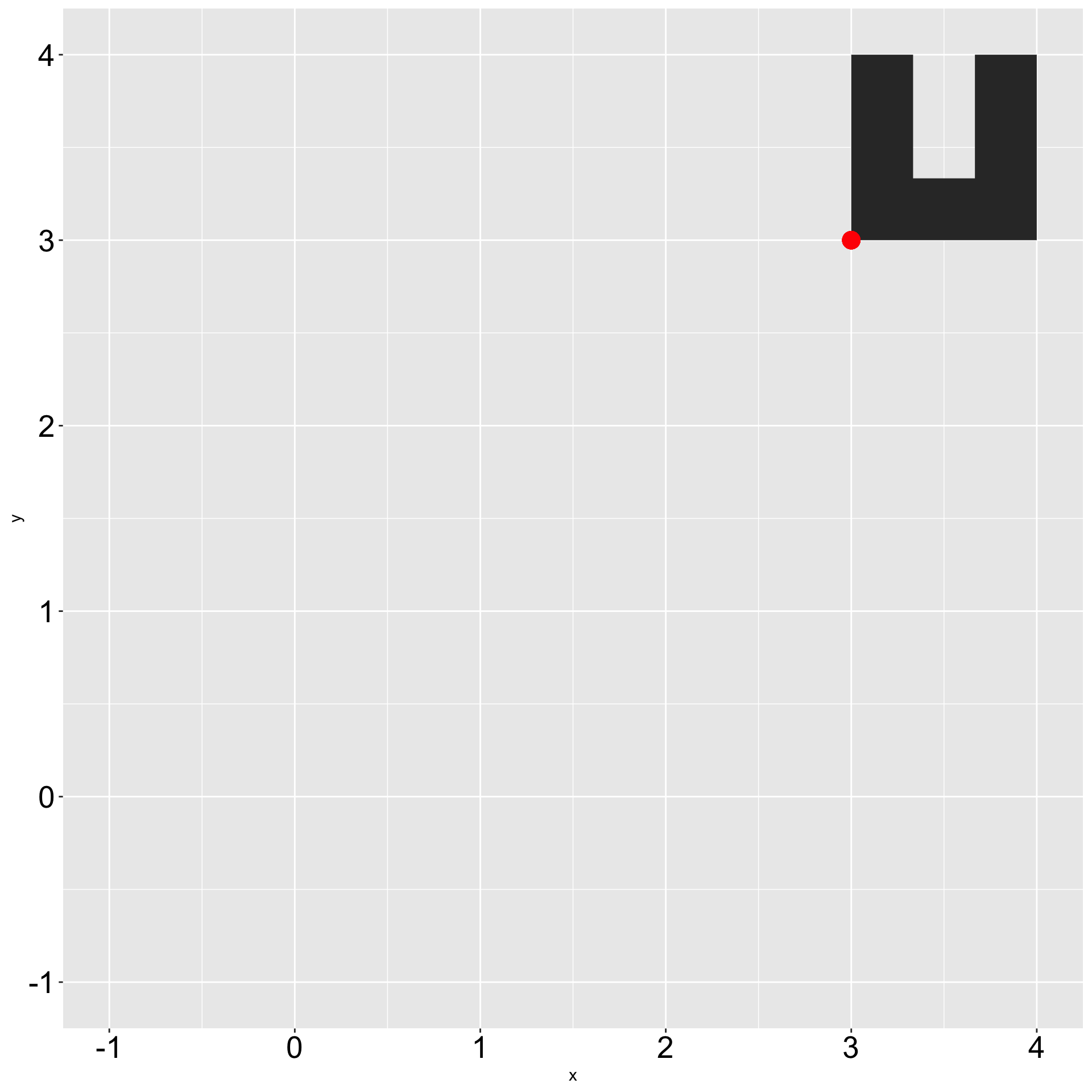
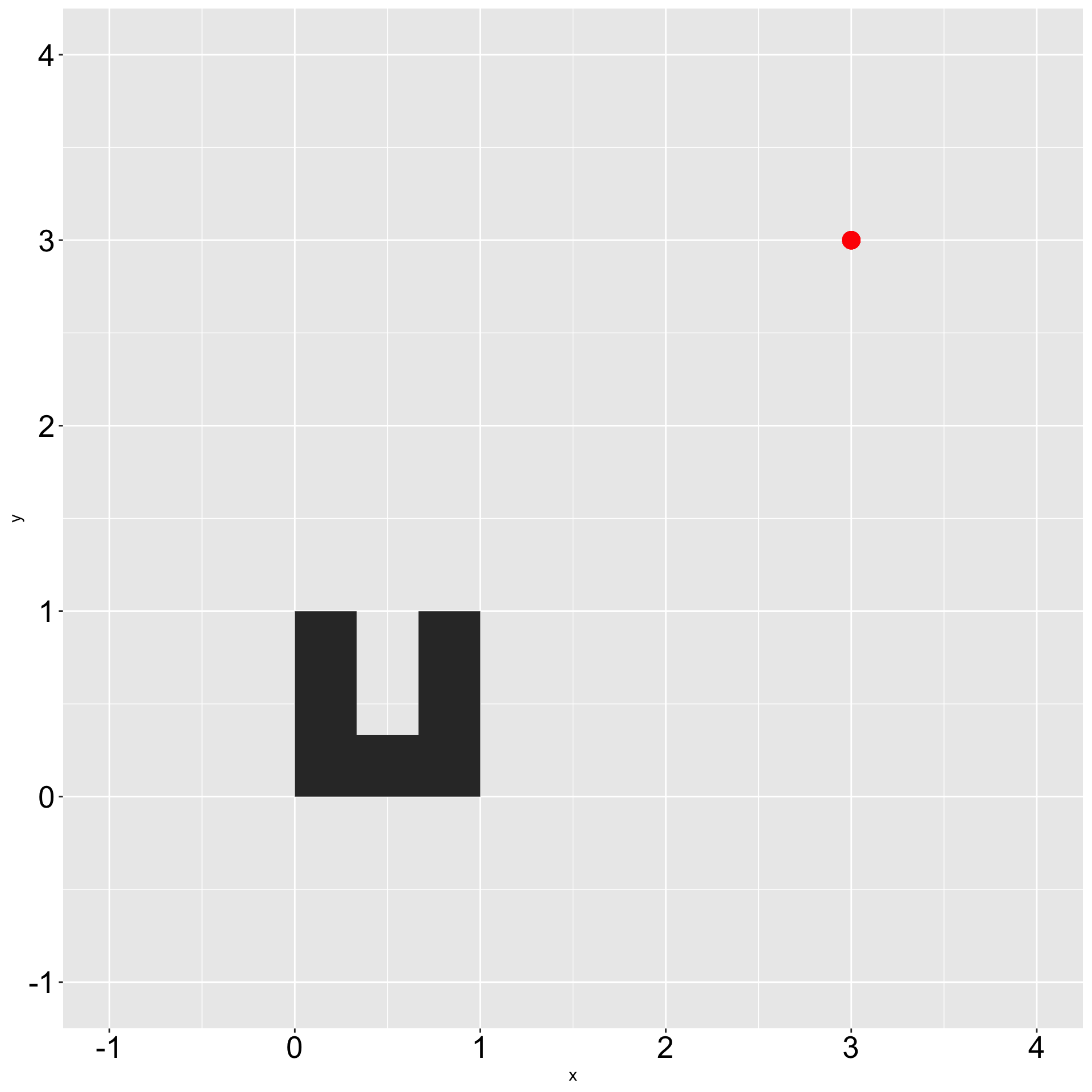
Applying trigonometry lesson
Step 1: Place shape
Applying trigonometry lesson
Step 2: Subtract point of rotation off of each vertex
Applying trigonometry lesson
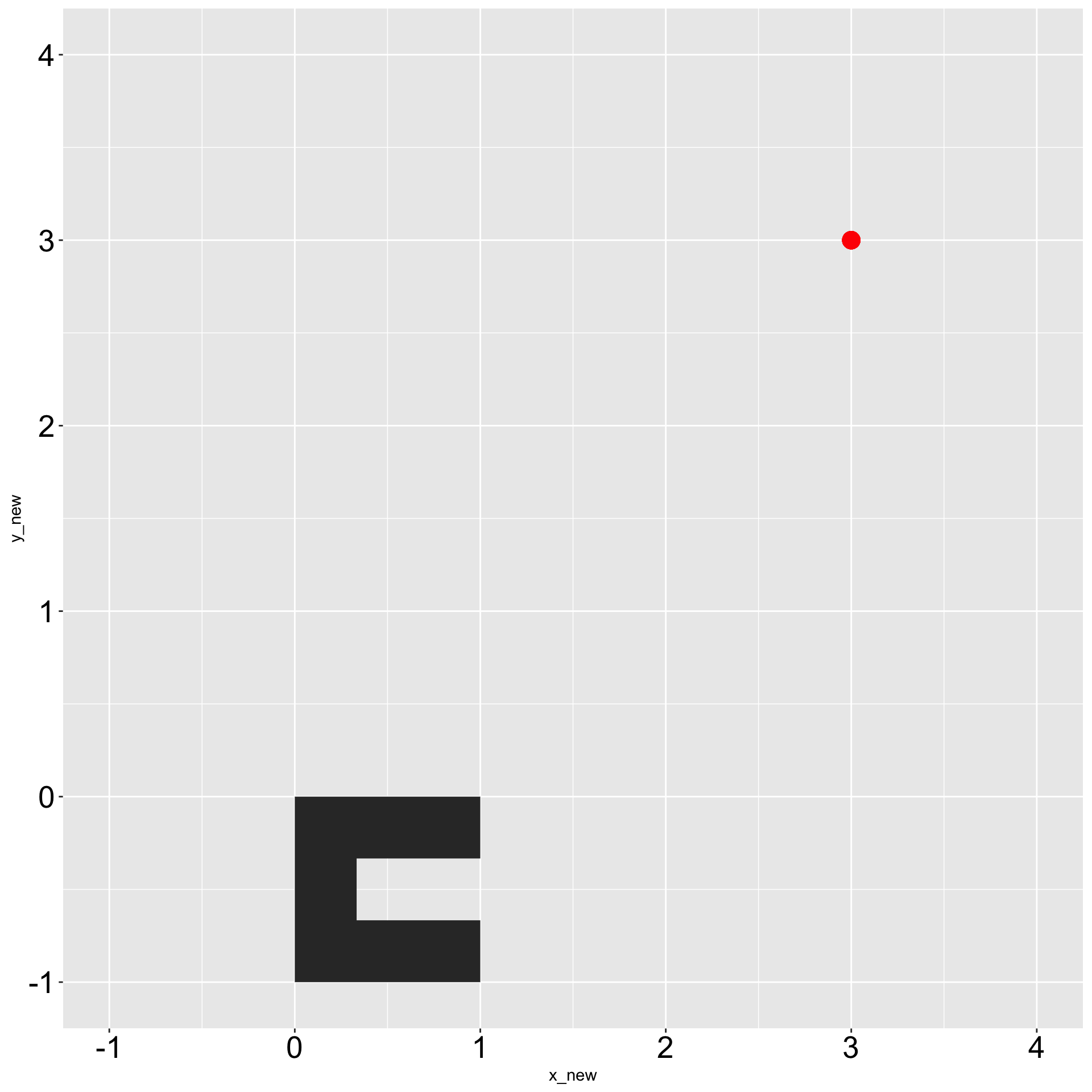
Step 3: Rotate
x0 <- 3
y0 <- 3
initial_u_shape <-
create_initial_shape(x0, y0) %>%
mutate(
x = x - x0,
y = y - y0
) %>%
mutate(
x_new = y,
y_new = -x
)
initial_u_shape %>%
ggplot() +
geom_polygon(
aes(
x = x_new,
y = y_new
)
) +
geom_point(
aes(
x = x0,
y = y0
),
size = 5,
color = "red"
) +
coord_fixed(
xlim = c(-1, 4),
ylim = c(-1, 4)
)
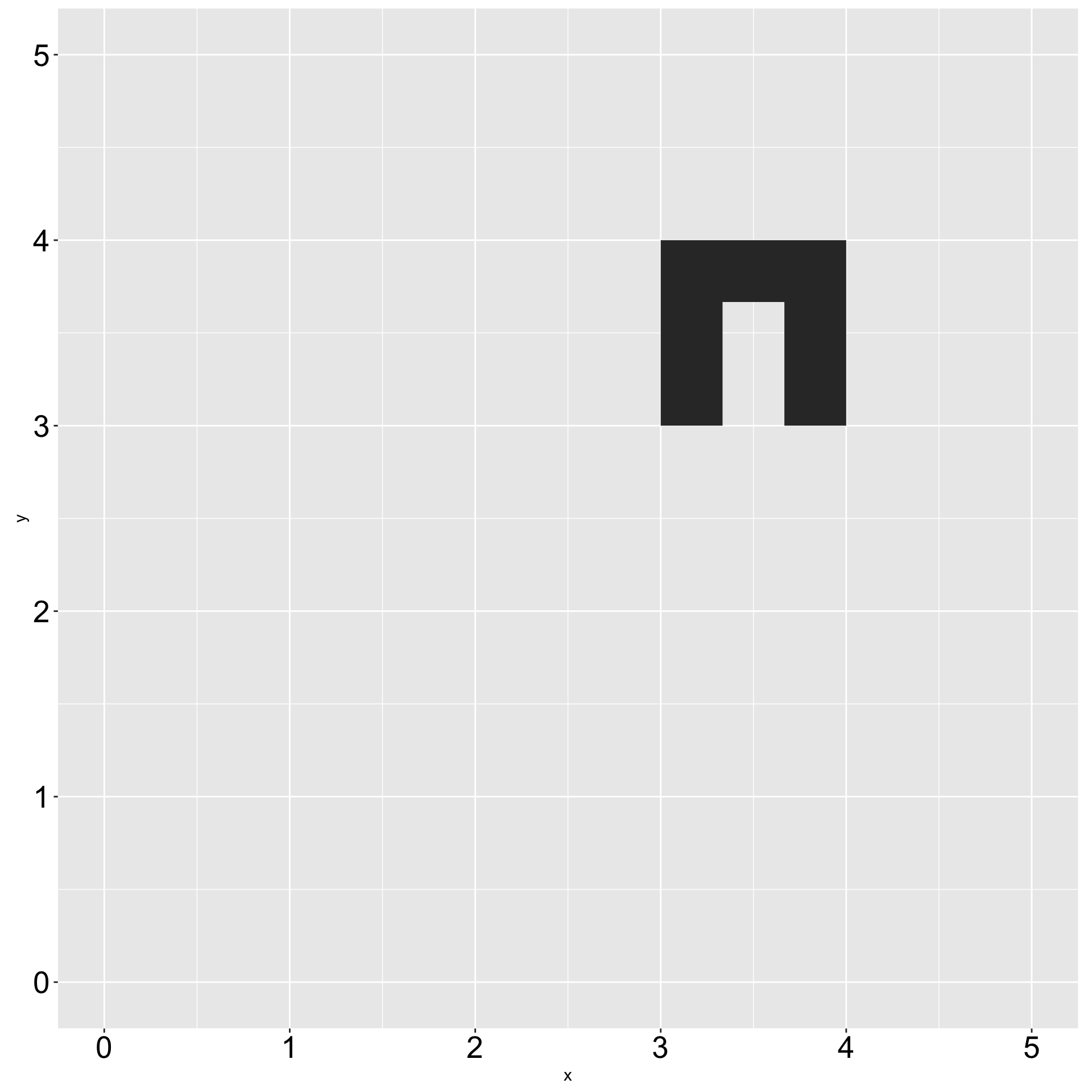
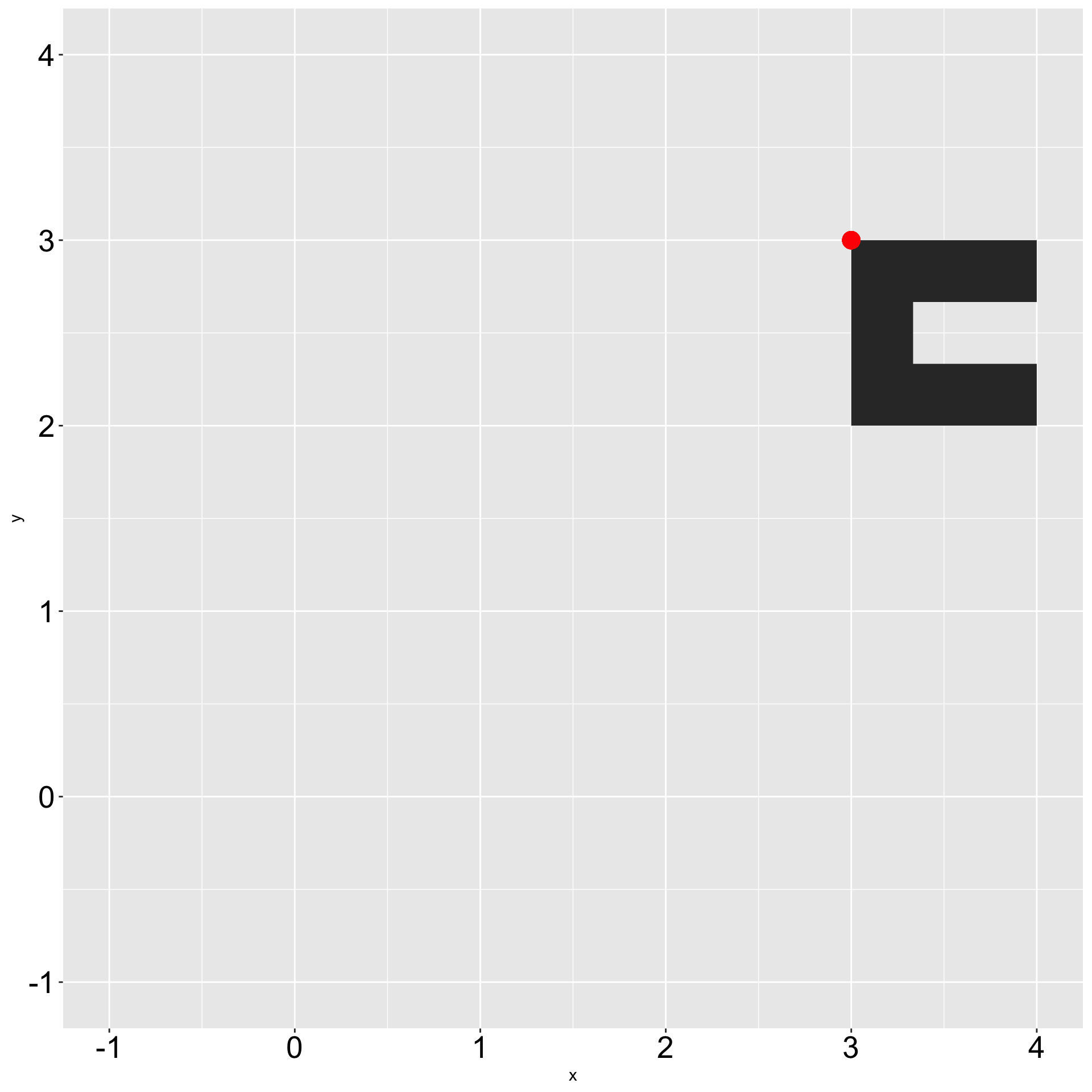
Applying trigonometry lesson
Step 4: Add back point of rotation
x0 <- 3
y0 <- 3
initial_u_shape <-
create_initial_shape(x0, y0) %>%
mutate(
x = x - x0,
y = y - y0
) %>%
mutate(
x_new = y,
y_new = -x
) %>%
mutate(
x = x_new + x0,
y = y_new + y0
)
initial_u_shape %>%
ggplot() +
geom_polygon(
aes(
x = x,
y = y
)
) +
geom_point(
aes(
x = x0,
y = y0
),
size = 5,
color = "red"
) +
coord_fixed(
xlim = c(-1, 4),
ylim = c(-1, 4)
)
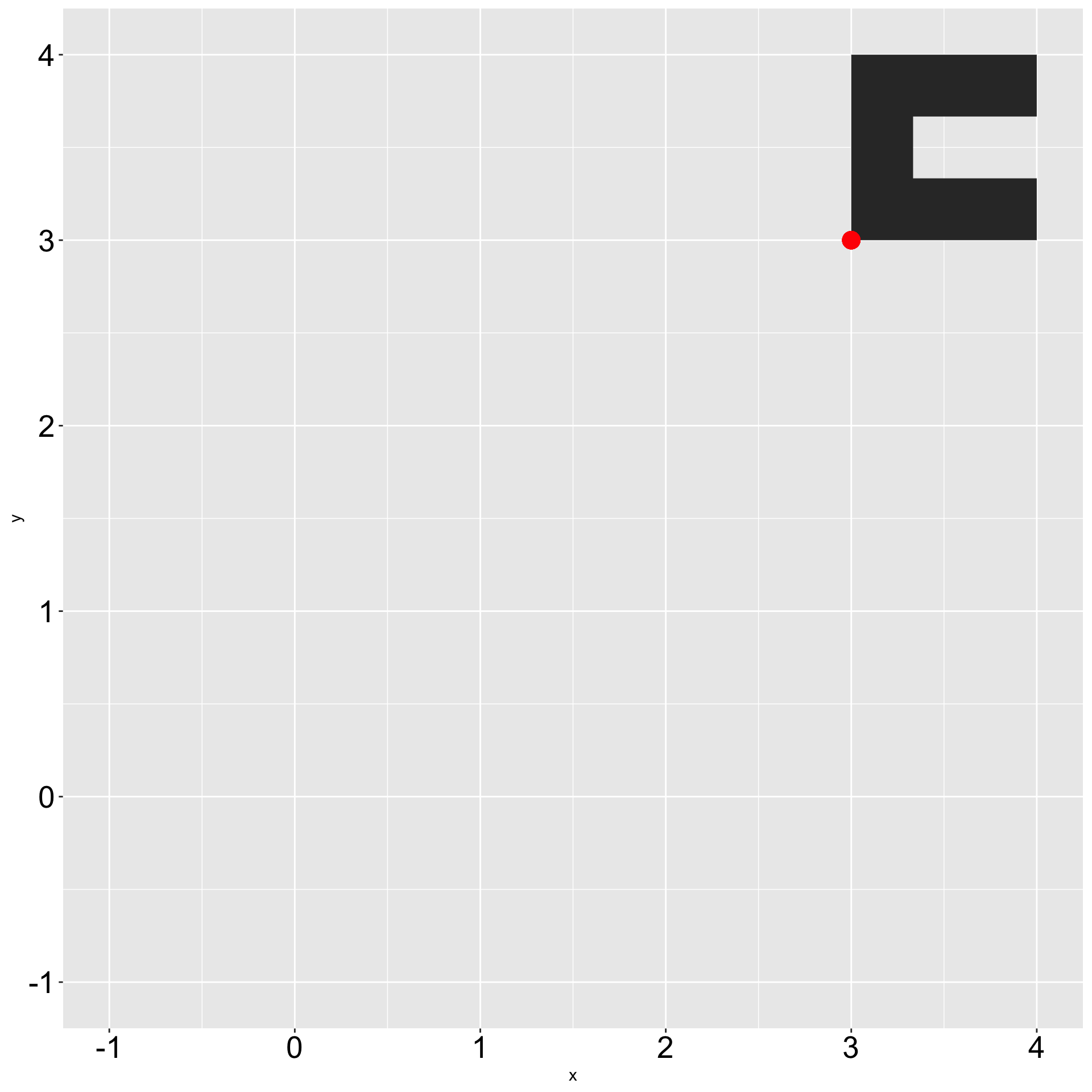
Applying trigonometry lesson
Step 5: Correct coordinates to back at “original origin”
x0 <- 3
y0 <- 3
shape_width <- 1
initial_u_shape <-
create_initial_shape(x0, y0) %>%
mutate(
x = x - x0,
y = y - y0
) %>%
mutate(
x_new = y,
y_new = -x
) %>%
mutate(
x = x_new + x0,
y = y_new + y0 + shape_width
)
initial_u_shape %>%
ggplot() +
geom_polygon(
aes(
x = x,
y = y
)
) +
geom_point(
aes(
x = x0,
y = y0
),
size = 5,
color = "red"
) +
coord_fixed(
xlim = c(-1, 4),
ylim = c(-1, 4)
)
Turning lesson into a function
rotate_shape <- function(data, x0, y0, degrees, shape_width) {
if (degrees == 90) {
data %>%
mutate(
x = x - x0,
y = y - y0
) %>%
mutate(
x_new = y,
y_new = -x
) %>%
mutate(
x = x_new + x0,
y = y_new + y0 + shape_width
)
} else if (degrees == 180) {
data %>%
mutate(
x = x - x0,
y = y - y0
) %>%
mutate(
x_new = -x,
y_new = -y
) %>%
mutate(
x = x_new + x0 + shape_width,
y = y_new + y0 + shape_width
)
} else if (degrees == 270) {
data %>%
mutate(
x = x - x0,
y = y - y0
) %>%
mutate(
x_new = -y,
y_new = x
) %>%
mutate(
x = x_new + x0 + shape_width,
y = y_new + y0
)
} else if (degrees == 0) {
data
}
}Turning lesson[s] into function[s]
Turning lesson[s] into function[s]
Exercise 2
- Reopen file if needed:
exercises/03-ot/exercise.Rmd
- If you closed the file after the previous exercise, you may need to first re-run the code chunks from Exercise 1.
- Run the code chunks to have access to the
initiate_rotate_shape()function. - Experiment with changing the
x0,y0, and thedegreesargument withininitiate_rotate_shape()to rotate and move your letter. - What happens if you change
shape_widthto be greater or smaller than 1? Why does this happen? - Remember to save your file when you are done with the exercise.
05:00
Composition of piece
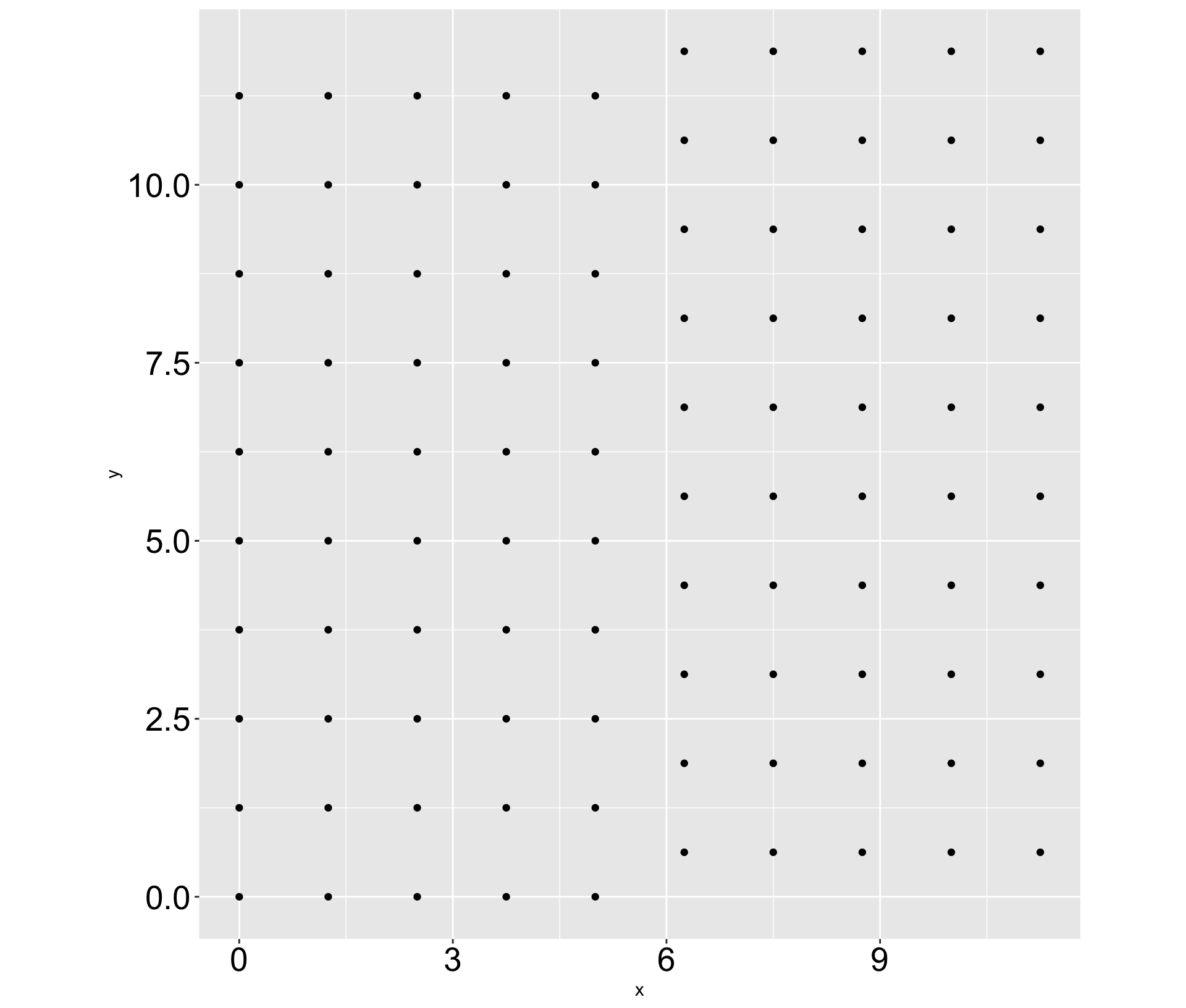
Creating the grid
Creating the grid
# A tibble: 100 × 2
x y
<dbl> <dbl>
1 0 0
2 0 1.25
3 0 2.5
4 0 3.75
5 0 5
6 0 6.25
7 0 7.5
8 0 8.75
9 0 10
10 0 11.2
# ℹ 90 more rowsCreating the grid
ncol <- 10
nrow <- 10
shape_width <- 1
perimeter_width <- shape_width + .25
grid <-
expand_grid(
x = seq(0,
by = perimeter_width,
length.out = ncol
),
y = seq(0,
by = perimeter_width,
length.out = nrow
)
) %>%
mutate(y = if_else(x >= 5 * perimeter_width,
y + perimeter_width / 2,
y
))
grid# A tibble: 100 × 2
x y
<dbl> <dbl>
1 0 0
2 0 1.25
3 0 2.5
4 0 3.75
5 0 5
6 0 6.25
7 0 7.5
8 0 8.75
9 0 10
10 0 11.2
# ℹ 90 more rowsCreating our system
library(purrr)
make_molnar_system <- function() {
ncol <- 10
nrow <- 10
shape_width <- 1
perimeter_width <- shape_width + .25
grid <-
expand_grid(
x = seq(0, by = perimeter_width, length.out = ncol),
y = seq(0, by = perimeter_width, length.out = nrow)
) %>%
mutate(y = if_else(x >= 5 * perimeter_width,
y + perimeter_width / 2,
y
))
output <-
map_dfr(
1:nrow(grid),
function(i) {
create_rotate_shape(
x = grid$x[i],
y = grid$y[i],
degrees = 180,
shape_width = shape_width
)
}
)
return(output)
}Applying our system
Creating polygons in {ggplot2}
geom_polygon()
We will use the following aesthetics
- coordinates of data (
x,y) - color of the border of the polygon (
color) - color of the inside of the polygon (
fill) - which coordinates belong to which polygon (
group)
Applying our system
Using group argument
make_molnar_system <- function() {
ncol <- 10
nrow <- 10
shape_width <- 1
perimeter_width <- shape_width + .25
grid <-
expand_grid(
x = seq(0, by = perimeter_width, length.out = nrow),
y = seq(0, by = perimeter_width, length.out = ncol)
) %>%
mutate(y = if_else(x >= 5 * perimeter_width,
y + perimeter_width / 2,
y
))
output <-
map_dfr(
1:nrow(grid),
function(i) {
bind_cols(
group = i,
create_rotate_shape(
x = grid$x[i],
y = grid$y[i],
degrees = 180,
shape_width = shape_width
)
)
}
)
return(output)
}Applying our system
Applying our system
Incorporating rotation
make_molnar_system <- function(seed) {
set.seed(seed)
ncol <- 10
nrow <- 10
shape_width <- 1
perimeter_width <- shape_width + .25
grid <-
expand_grid(
x = seq(0, by = perimeter_width, length.out = nrow),
y = seq(0, by = perimeter_width, length.out = ncol)
) %>%
mutate(y = if_else(x >= 5 * perimeter_width,
y + perimeter_width / 2,
y
))
output <-
map_dfr(
1:nrow(grid),
function(i) {
bind_cols(
group = i,
create_rotate_shape(
x = grid$x[i],
y = grid$y[i],
degrees = 180,
shape_width = shape_width
)
)
}
)
return(output)
}Applying our system
Incorporating rotation
make_molnar_system <- function(seed) {
set.seed(seed)
ncol <- 10
nrow <- 10
shape_width <- 1
perimeter_width <- shape_width + .25
grid <-
expand_grid(
x = seq(0, by = perimeter_width, length.out = nrow),
y = seq(0, by = perimeter_width, length.out = ncol)
) %>%
mutate(y = if_else(x >= 5 * perimeter_width,
y + perimeter_width / 2,
y
))
output <-
map_dfr(
1:nrow(grid),
function(i) {
bind_cols(
group = i,
create_rotate_shape(
x = grid$x[i],
y = grid$y[i],
degrees = sample(c(0, 90, 180, 270),
size = 1
),
shape_width = shape_width
)
)
}
)
return(output)
}Applying our system
Incorporating rotation
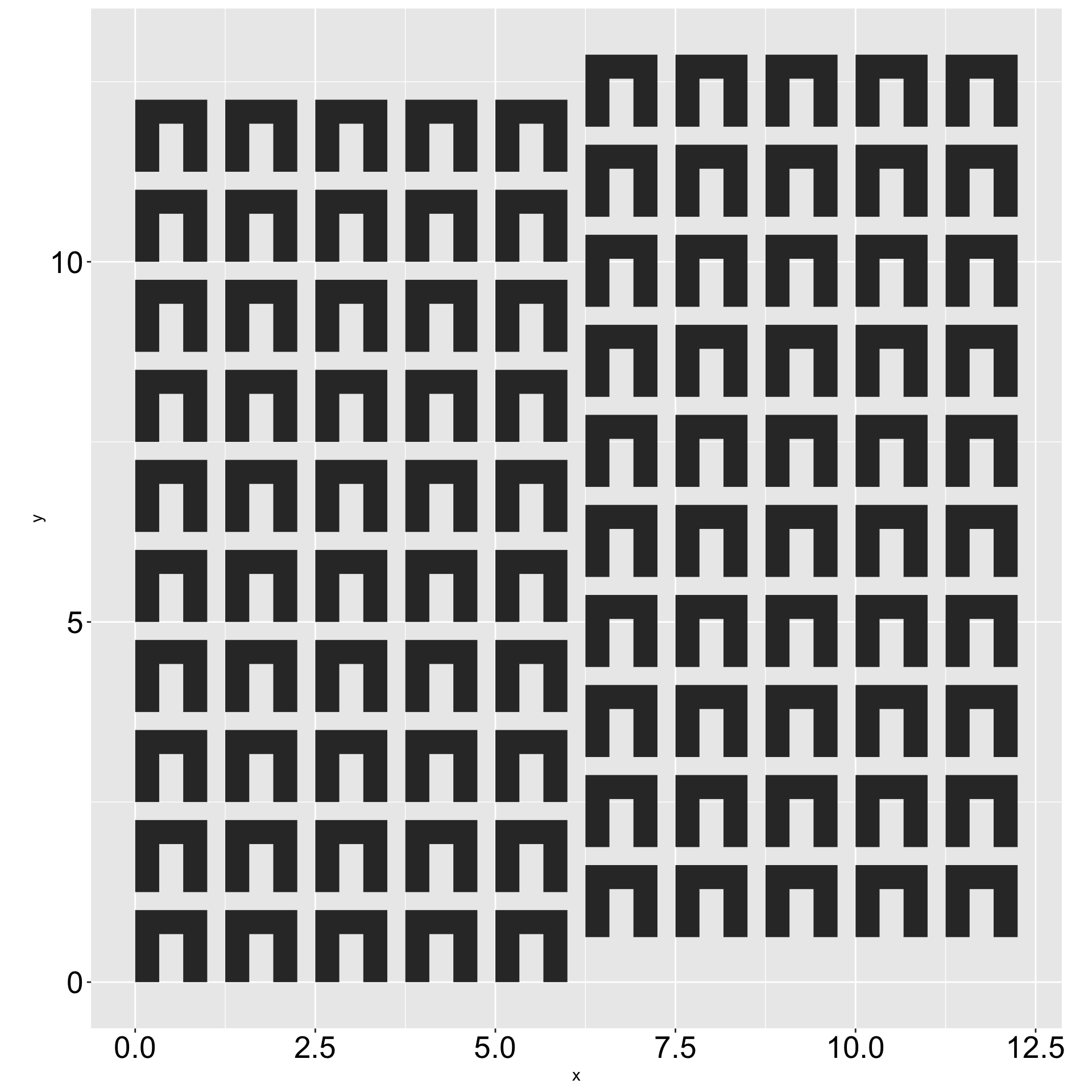
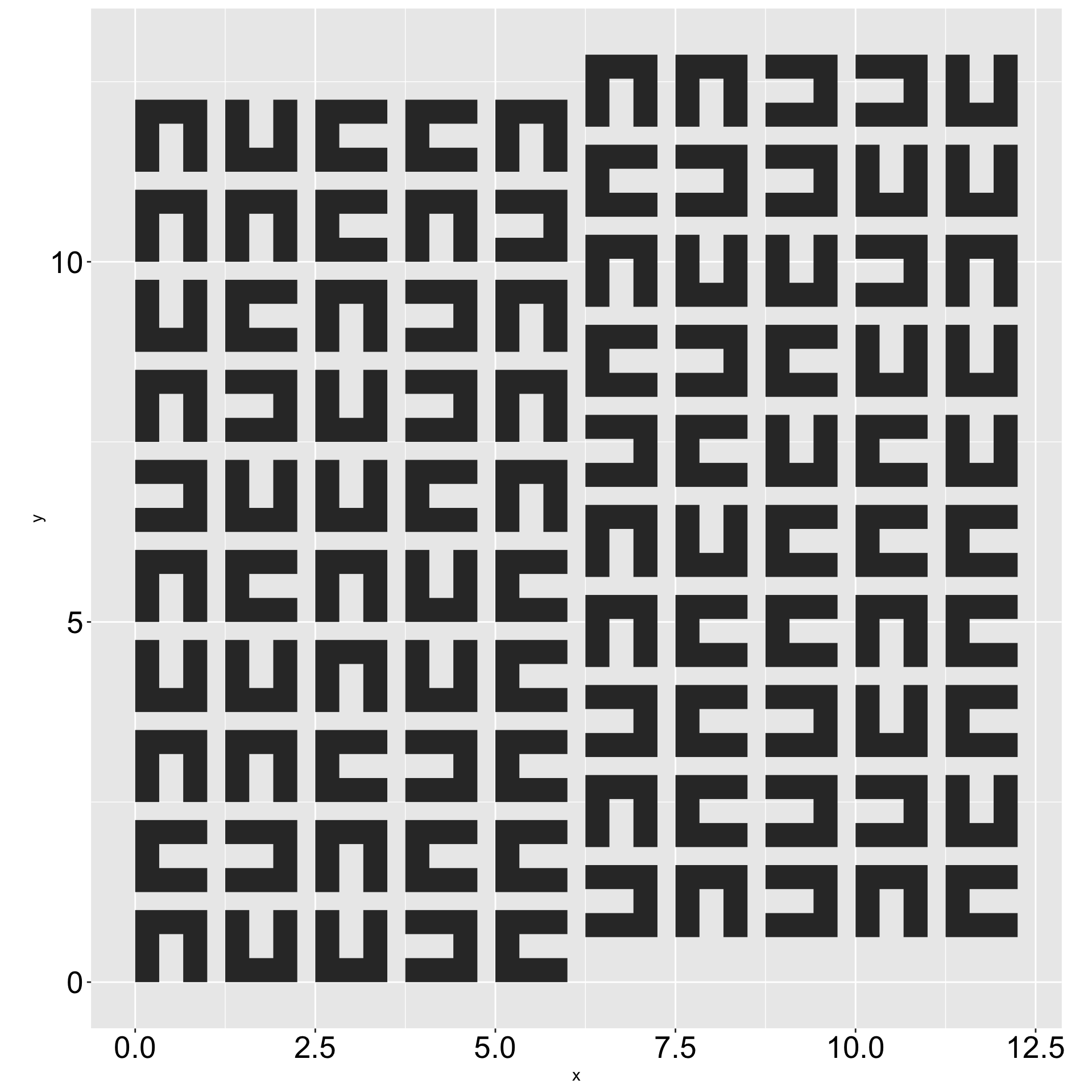
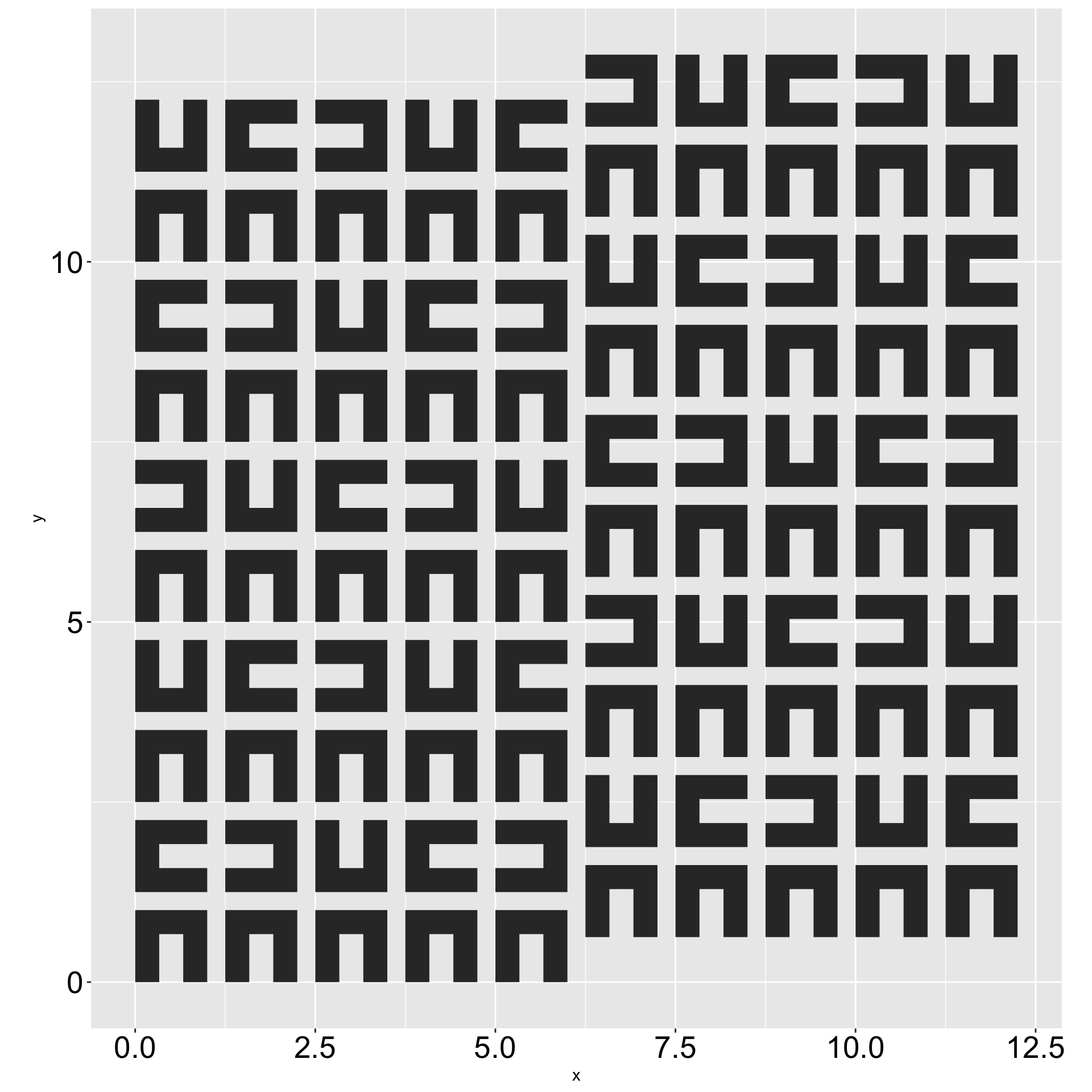
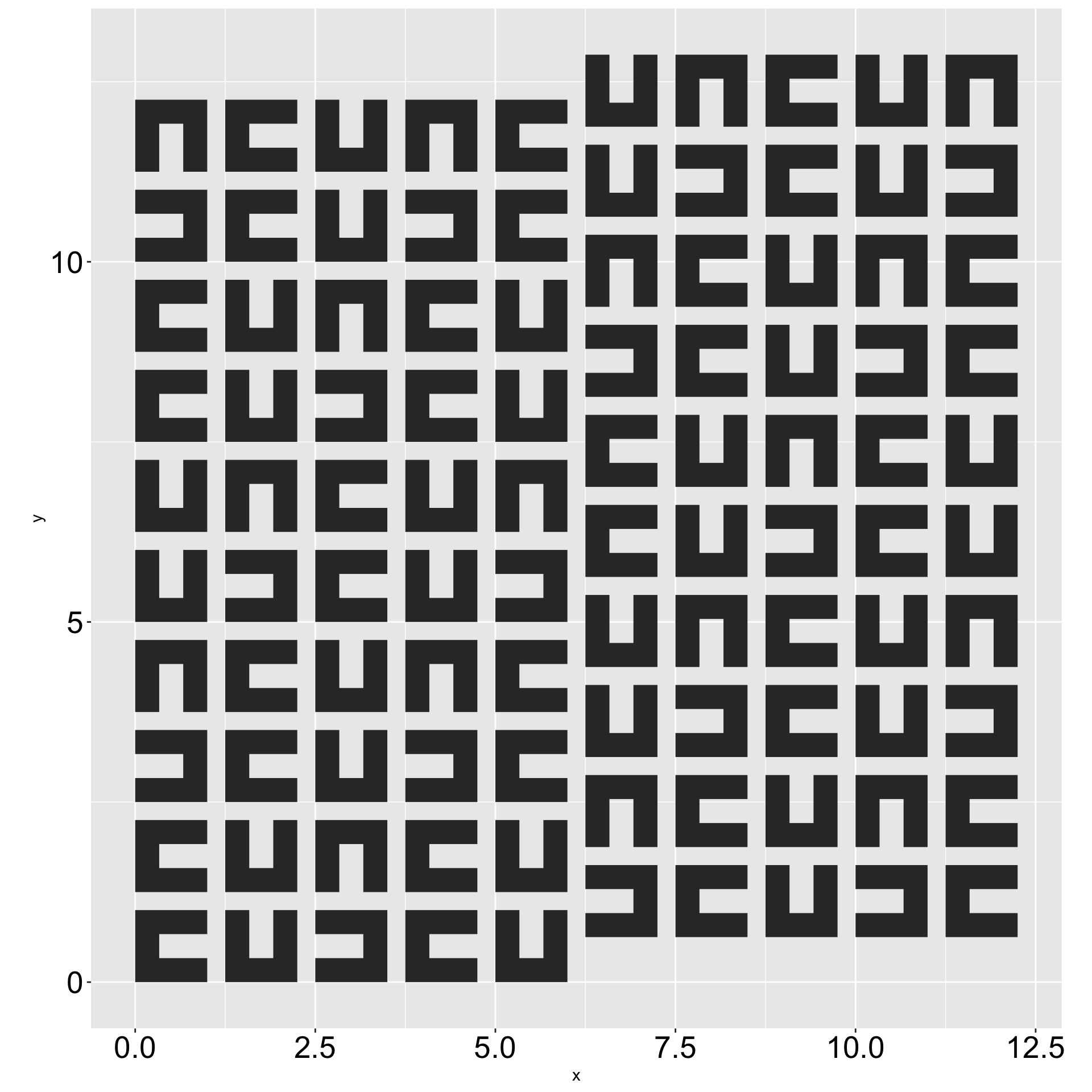
Patterns vs. Pure Random


Patterns vs. Pure Random


Patterns vs. Pure Random

Layout: 1, 2, 3, Skip, 4, 1, 2
Patterns vs. Pure Random
Patterns vs. Pure Random
Patterns vs. Pure Random
make_molnar_system <-
function(seed) {
set.seed(seed)
ncol <- 10
nrow <- 10
shape_width <- 1
perimeter_width <- shape_width + .25
degree_pattern_options <- c(0, 90, 180, 270)
degree_pattern <- sample(degree_pattern_options, size = 6, replace = TRUE)
grid <-
expand_grid(
x = seq(0,
by = perimeter_width,
length.out = nrow
),
y = seq(0,
by = perimeter_width,
length.out = ncol
)
) %>%
mutate(y = if_else(x >= 5 * perimeter_width,
y + perimeter_width / 2,
y
))
degree_pattern_exp <- rep(degree_pattern,
length.out = nrow(grid)
)
output <-
map_dfr(
1:nrow(grid),
function(i) {
bind_cols(
group = i,
create_rotate_shape(
x = grid$x[i],
y = grid$y[i],
degrees = degree_pattern_exp[i],
shape_width = shape_width
)
)
}
)
return(output)
}Patterns vs. Pure Random
Patterns vs. Pure Random
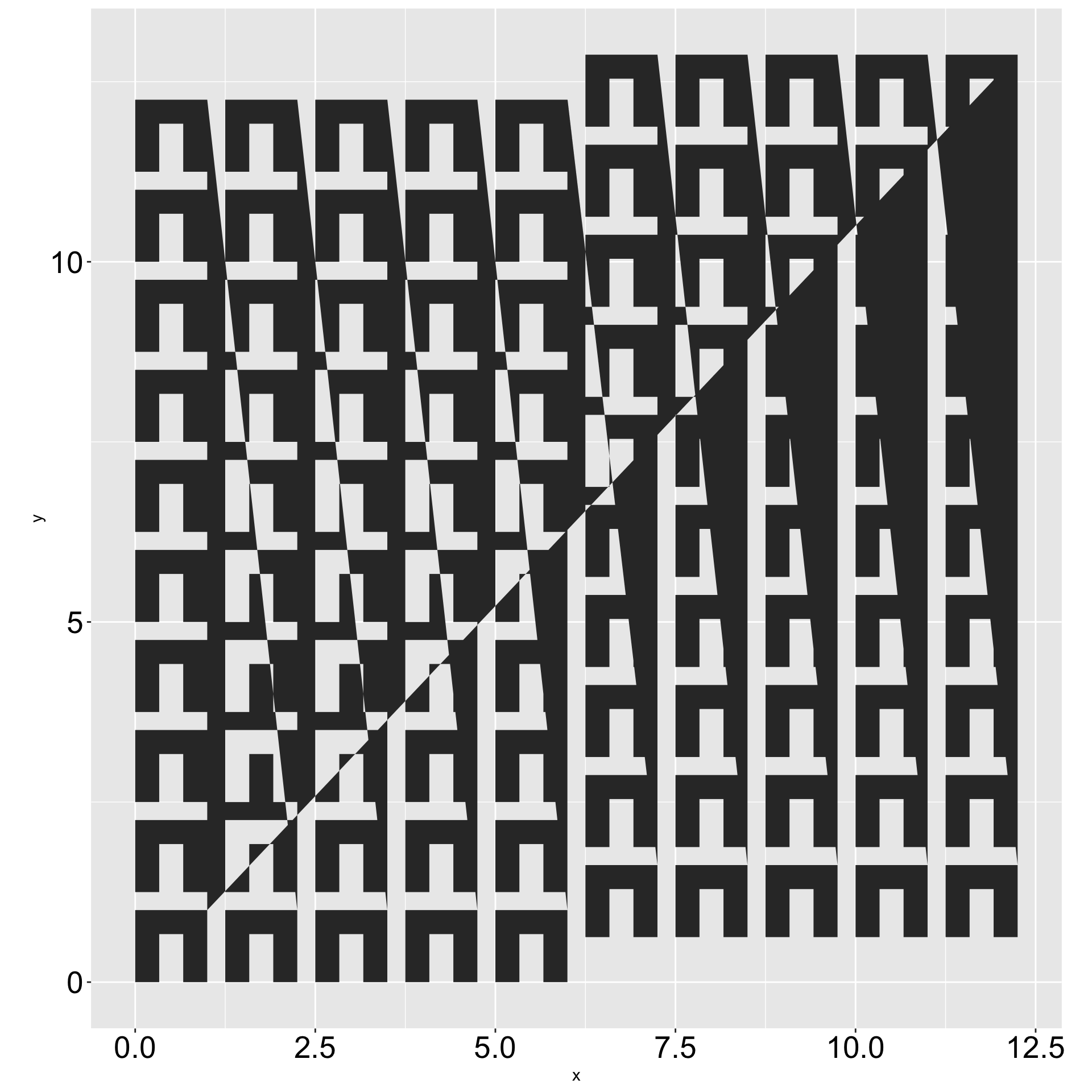
Final Touches
Final Piece
Final Piece
Final Piece
Final Piece


Exercise 3
- Reopen file if needed:
exercises/03-ot/exercise.Rmd - Review the code chunk that contains the
make_exercise_molnar()function which encompasses the whole system. - Update the arguments
degree_pattern_options=anddegree_sample_size=for the functionmake_exercise_molnar()to experiment with modifying the rotation patterns to one of your choice. (Degrees options are 0, 90, 80, 270) - Save your image using
ggsave()code provided and share on GitHub discussion board. - If you have extra time, here are some suggestion for customizing your piece:
- Experiment with colors in the
fill=andcolor=ingeom_polygon() - Experiment with colors in the
plot.backgroundintheme()
10:00
Recap
- Created a shape using
geom_polygon() - Explored the intricacies of
geom_polygon()arguments: order matters and group is important! - Rotated a shape 0, 90, 180, and 270 degrees using trigonometry
- Explored implementing pure randomness or randomness to create patterns